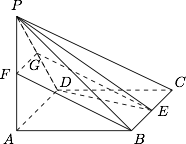
已知四棱锥 $P - ABCD$ 的底面是边长为 $2$ 的菱形,且 $\angle BAD = 60^\circ $,$PA \perp ABCD$,且 $PA = 1$,$E$,$F$ 分别是 $BC$,$PA$ 的中点.
【难度】
【出处】
2006年武汉大学自主招生保送生测试
【标注】
-
求证:$BF\parallel PED$;标注答案略解析取 $PD$ 中点,记为 $G$,则四边形 $BEGF$ 为平行四边形,所以 $BF\parallel NG$,因此 $BF\parallel PED$.
-
求二面角 $P - DE - A$ 的大小;标注答案$\arctan \dfrac{1}{2}$解析因为 $\angle BAD=60^\circ$,所以在菱形 $ABCD$ 中,$$AD\perp DE.$$因为 $PA\perp $ 平面 $ABCD$,所以 $\angle PDA$ 即为二面角 $P - DE - A$ 的平面角.
因为$$\tan \angle PDA=\dfrac {PA}{AD}=\dfrac 12,$$所以二面角 $P - DE - A$ 的大小为 $\arctan \dfrac 12$. -
求点 $C$ 到平面 $PED$ 的距离.标注答案$\dfrac{{\sqrt 5 }}{5}$解析利用等体积法.四面体 $P-CDE$ 的体积为$$V=\dfrac 13\cdot S_{\triangle CDE}\cdot PA=\dfrac {\sqrt 3}{6}.$$因为 $ED\perp PA$,$ED\perp AD$,所以 $ED\perp PD$,所以 $\triangle PED$ 的面积为$$S=\dfrac 12\cdot PD\cdot ED=\dfrac {\sqrt {15}}{2}.$$设 $C$ 到平面 $PDE$ 的距离为 $d$,$$V=\dfrac 13\cdot S\cdot d,$$解得 $d=\dfrac {\sqrt 5}{5}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3