如图1，矩形 $ ABCD $ 中，$AB=7 \mathrm {cm}$，$AD=4 \mathrm {cm}$，点 $E$ 为 $AD$ 上一定点，点 $F$ 为 $AD$ 延长线上一点，且 $DF=a \mathrm {cm}$．点 $P$ 从 $A$ 点出发，沿 $AB$ 边向点 $B$ 以 $2 \mathrm {cm{/}s}$ 的速度运动．连接 $PE$，设点 $P$ 运动的时间为 $t \mathrm s$，$\triangle PAE$ 的面积为 $y \mathrm {cm^2}$．当 $0\leqslant t\leqslant 1$ 时，$\triangle PAE$ 的面积 $y\left(\mathrm {cm^2}\right)$ 关于时间 $t\left(\mathrm s\right)$ 的函数图象如图2所示．连接 $PF$，交 $CD$ 于点 $H$．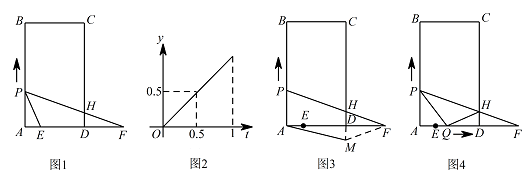
【难度】
【出处】
无
【标注】
-
如图3，将 $\triangle HDF$ 沿线段 $DF$ 进行翻折，与 $CD$ 的延长线交于点 $M$，连接 $AM$．当 $a$ 为何值时，四边形 $PAMH$ 为菱形？并求出此时点 $P$ 的运动时间 $t$；标注答案当 $a=4$ 时，四边形 $PAMH$ 为菱形，此时点 $P$ 的运动时间为 $\dfrac {4\sqrt 3} 3 \mathrm s$解析若四边形 $PAMH$ 为菱形，则 $PA\parallel HM$，且 $PA=HM$，$AM=HM$．
因为 $\triangle MDF$ 是由 $\triangle HDF$ 沿线段 $DF$ 进行翻折而得，
所以 $\angle HDF=\angle ADM=90^{\circ}$，$HD=DM$．
又 $DH\parallel AP$，
所以 $\triangle PAF\backsim \triangle HDF$．
从而 $\dfrac{HD}{PA}=\dfrac{FD}{AF}=\dfrac 12$．
而 $DF=a$，所以 $AF=4+a$，
所以 $\dfrac a{a+4}=\dfrac 12$，解得 $a=4$．
在直角三角形 $ADM$ 中，$AM=PA=2t$，$AM^2=DM^2+AD^2$，
所以 $4t^2=4^2+t^2$，解得 $t=\dfrac {4\sqrt 3}3$．
所以当 $a=4$ 时，四边形 $PAMH$ 为菱形，此时点 $P$ 的运动时间为 $\dfrac {4\sqrt 3} 3 \left(\mathrm s\right)$． -
如图4，当点 $P$ 出发 $1 \mathrm s$ 后，$AD$ 边上另一点 $Q$ 从 $E$ 点出发，沿 $ED$ 边向点 $D$ 以 $1 \mathrm {cm{/}s}$ 的速度运动．如果 $P$，$Q$ 两点中的任意一点到达终点后，另一点也停止运动．连接 $PQ,QH$．若 $a=\dfrac 4 3 \mathrm {cm}$，请问 $\triangle PQH$ 能否构成直角三角形？若能，请求出点 $P$ 的运动时间 $t$；若不能，请说明理由．标注答案当 $t=2$ 或 $t=\dfrac 8 3 $ 时，$\triangle PQH$ 为直角三角形解析
解法一 当 $a=\dfrac 4 3 $ 时，由题意，得 $AQ=t$，$QD=4-t$．
因为 $DH\parallel AP $，
所以 $\triangle PAF\backsim \triangle HDF$．
所以 $\dfrac{HD}{PA}=\dfrac{DF}{AF}$，即 $\dfrac{\dfrac 43} {4+\dfrac 43}=\dfrac 14$，
从而 $HD=\dfrac 1 4 \times 2t=\dfrac t 2 $．
过点 $P$ 作 $PG$ 垂直于 $CD$，垂足为点 $G$．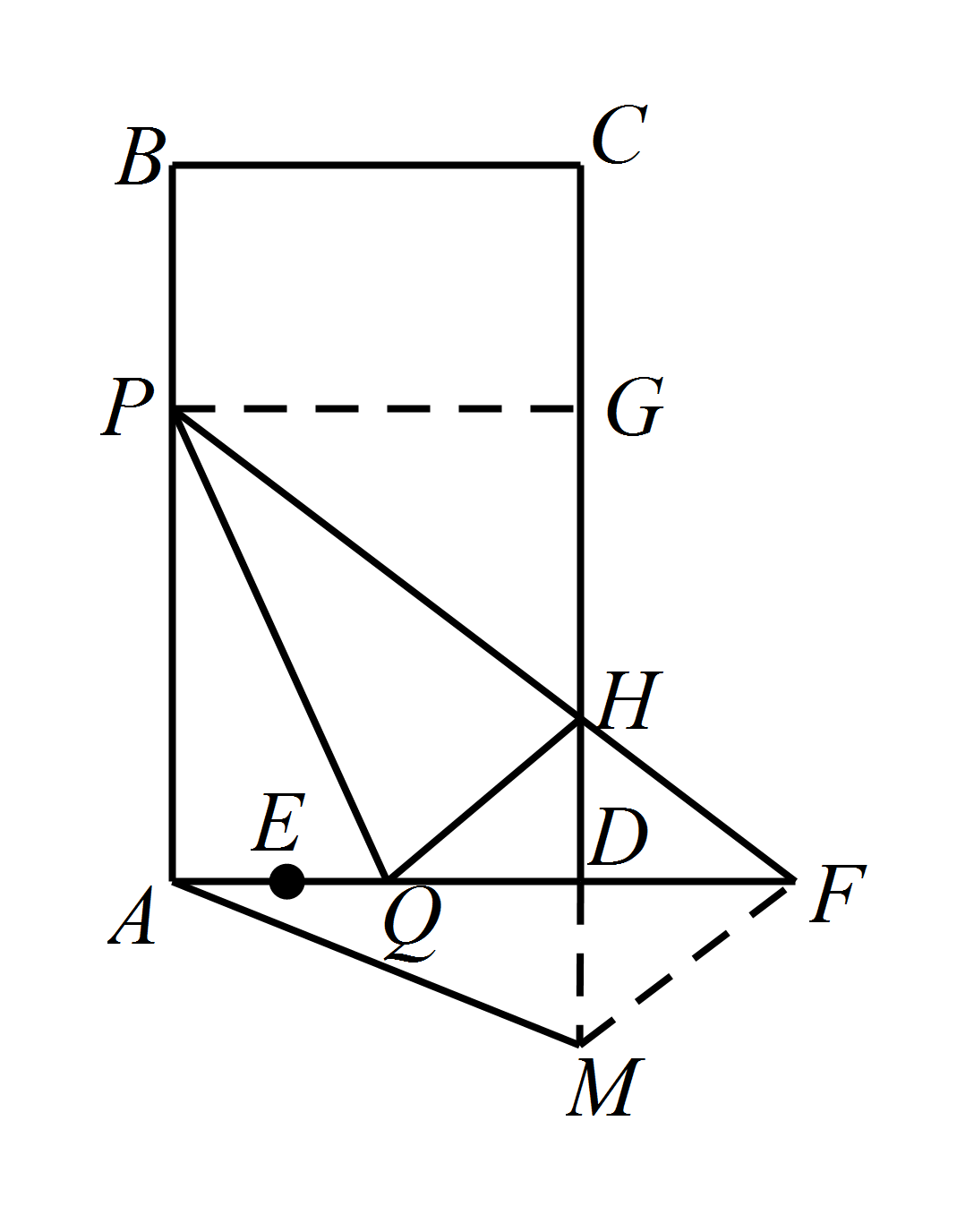
则 $GH=2t-\dfrac t 2 =\dfrac 3 2 t$，$PQ^2=PA^2+AQ^2=5t^2$，$QH^2=QD^2+HD^2=\left(4-t\right)^2+\dfrac 1 4 t^2$，
$PH^2=PG^2+HG^2=16+\dfrac 9 4 t^2$．
若 $\triangle PQH$ 为直角三角形，
① 当 $Q$ 为直角顶点时，则 $5t^2+\left(4-t\right)^2+\dfrac 1 4 t^2=16+\dfrac 9 4 t^2$，
解得 $t=2$ 或 $t=0$（舍去）．
② 当 $H$ 为直角顶点时，则 $16+\dfrac 9 4 t^2+\left(4-t\right)^2+\dfrac 1 4 t^2=5t^2$，
解得 $t=\dfrac 8 3 $ 或 $t=-8$（舍去）．
③ 当 $P$ 为直角顶点时，则 $5t^2+16+\dfrac 9 4 t^2=\left(4-t\right)^2+\dfrac 1 4 t^2$，
解得 $t=-\dfrac 4 3 $（舍去）或 $t=0$（舍去）．
所以当 $t=2$ 或 $t=\dfrac 8 3$ 时，$\triangle PQH$ 为直角三角形．解法二 由题意可知，$PA=2t$，$ AQ=t $，$ HD=\dfrac t 2 $，$ QD=4-t $，$HG=\dfrac 3 2 t$．
若 $\triangle PQH$ 为直角三角形，
① 当 $Q$ 为直角顶点时，
由 $\triangle PAQ\backsim \triangle QDH$，则 $\dfrac{PA}{QD}=\dfrac{AQ}{HD}$，
即 $\dfrac{2t}{4-t}=\dfrac t{\dfrac t2}$，解得 $t=2$．
② 当 $H$ 为直角顶点时，
由 $\triangle QHD\backsim \triangle HFD$，则 $\dfrac{QD}{HD}=\dfrac{HD}{DF}$，
即 $\dfrac{4-t}{\dfrac t2}=\dfrac{\dfrac t2} {\dfrac 43}$，解得 $t=\dfrac 83$，或 $t=-8$（舍去）．
③ 当 $P$ 为直角顶点时，不可能．
所以当 $t=2$ 或 $t=\dfrac 8 3 $ 时，$\triangle PQH$ 为直角三角形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
