莱洛三角形是著名的非圆等宽曲线，它的画法如下：先画一个正三角形 $ABC$，再分别以 $A,B,C$ 为圆心，作圆弧 $BC,CA,AB$，这三段弧围成的图形就是莱洛三角形，正三角形 $ABC$ 的边长称为莱洛三角形的宽度，如图所示．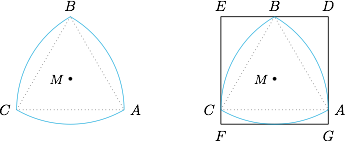
现有宽度为 $1$ 的莱洛三角形嵌在一个边长为 $1$ 的正方形内部，即正方形的各边上都有莱洛三角形边缘上的点．当莱洛三角形的三个顶点沿着正方形边界行进一周的过程中，求正三角形 $ABC$ 的中心 $M$ 的轨迹方程．
现有宽度为 $1$ 的莱洛三角形嵌在一个边长为 $1$ 的正方形内部，即正方形的各边上都有莱洛三角形边缘上的点．当莱洛三角形的三个顶点沿着正方形边界行进一周的过程中，求正三角形 $ABC$ 的中心 $M$ 的轨迹方程．【难度】
【出处】
无
【标注】
【答案】
$12x^2+12y^2-12\sqrt{3}xy-6\left(2-\sqrt{3}\right)x-6\left(2-\sqrt{3}\right)y=3\sqrt{3}-5$，其中 $\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant x \leqslant 0$，$\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant y \leqslant 0$
【解析】
考虑莱洛三角形从图中的初始位置逆时针旋转 $\dfrac{\pi}{6}$ 的变化过程．
以正方形的中心为原点 $O$ 建立平面直角坐标系，设 $M(x,y)$，$\angle ABD=\theta \left(\dfrac{\pi}{6}\leqslant \theta \leqslant \dfrac{\pi}{3}\right)$，因为 $\overrightarrow{OM}=\overrightarrow{OB}+\overrightarrow{BM}$，所以\[\begin{split}
(x,y)
&=\left(\dfrac{1}{2}-\cos{\theta},\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{3}}{3}\cos{\left(-\dfrac{\pi}{6}-\theta\right)},\dfrac{\sqrt{3}}{3}\sin{\left(-\dfrac{\pi}{6}-\theta\right)}\right)\\
&=\left(\dfrac{1}{2}-\dfrac{1}{2}\cos{\theta}-\dfrac{\sqrt{3}}{6}\sin{\theta},\dfrac{1}{2}-\dfrac{1}{2}\sin{\theta}-\dfrac{\sqrt{3}}{6}\cos{\theta}\right),
\end{split}\]所以 $M$ 点轨迹的参数方程为\[\begin{split}\begin{cases}x=\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\sin{\left(\theta+\dfrac{\pi}{3}\right)},\\
y=\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\sin{\left(\theta+\dfrac{\pi}{6}\right)},
\end{cases}\end{split}\]其中参数 $\dfrac{\pi}{6}\leqslant \theta \leqslant \dfrac{\pi}{3}$．
消去 $\theta$，得其普通方程为\[
12x^2+12y^2-12\sqrt{3}xy-6\left(2-\sqrt{3}\right)x-6\left(2-\sqrt{3}\right)y=3\sqrt{3}-5,\]其中$$\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant x \leqslant 0,\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant y \leqslant 0.$$故此时 $M$ 点的轨迹是中心为 $\left(\dfrac{1}{2},\dfrac{1}{2}\right)$，半长轴为 $\dfrac{3+\sqrt{3}}{6}$，半短轴为 $\dfrac{3-\sqrt{3}}{6}$，焦点在直线 $y=x$ 上的椭圆 $\Gamma$ 位于第三象限的部分．
由对称性，同理可得其它三部分 $M$ 点的轨迹方程，它们表示的曲线都是与椭圆 $\Gamma$ 对称的椭圆在某一象限的一段弧．$M$ 的轨迹是由上述四个对称椭圆的四段弧组成的．
以正方形的中心为原点 $O$ 建立平面直角坐标系，设 $M(x,y)$，$\angle ABD=\theta \left(\dfrac{\pi}{6}\leqslant \theta \leqslant \dfrac{\pi}{3}\right)$，因为 $\overrightarrow{OM}=\overrightarrow{OB}+\overrightarrow{BM}$，所以\[\begin{split}
(x,y)
&=\left(\dfrac{1}{2}-\cos{\theta},\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{3}}{3}\cos{\left(-\dfrac{\pi}{6}-\theta\right)},\dfrac{\sqrt{3}}{3}\sin{\left(-\dfrac{\pi}{6}-\theta\right)}\right)\\
&=\left(\dfrac{1}{2}-\dfrac{1}{2}\cos{\theta}-\dfrac{\sqrt{3}}{6}\sin{\theta},\dfrac{1}{2}-\dfrac{1}{2}\sin{\theta}-\dfrac{\sqrt{3}}{6}\cos{\theta}\right),
\end{split}\]所以 $M$ 点轨迹的参数方程为\[\begin{split}\begin{cases}x=\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\sin{\left(\theta+\dfrac{\pi}{3}\right)},\\
y=\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\sin{\left(\theta+\dfrac{\pi}{6}\right)},
\end{cases}\end{split}\]其中参数 $\dfrac{\pi}{6}\leqslant \theta \leqslant \dfrac{\pi}{3}$．
消去 $\theta$，得其普通方程为\[
12x^2+12y^2-12\sqrt{3}xy-6\left(2-\sqrt{3}\right)x-6\left(2-\sqrt{3}\right)y=3\sqrt{3}-5,\]其中$$\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant x \leqslant 0,\dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\leqslant y \leqslant 0.$$故此时 $M$ 点的轨迹是中心为 $\left(\dfrac{1}{2},\dfrac{1}{2}\right)$，半长轴为 $\dfrac{3+\sqrt{3}}{6}$，半短轴为 $\dfrac{3-\sqrt{3}}{6}$，焦点在直线 $y=x$ 上的椭圆 $\Gamma$ 位于第三象限的部分．
由对称性，同理可得其它三部分 $M$ 点的轨迹方程，它们表示的曲线都是与椭圆 $\Gamma$ 对称的椭圆在某一象限的一段弧．$M$ 的轨迹是由上述四个对称椭圆的四段弧组成的．
答案
解析
备注
