如图,已知 $M$ 是线段 $AB$ 的中点,$CD,EF$ 相交于 $M$,又 $CF,ED$ 分别交 $AB$ 于 $P,Q$.求证:$\left|PM\right|=\left|QM\right|$.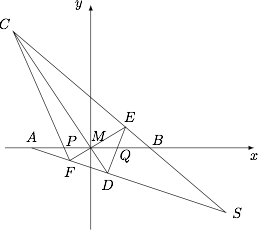

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设直线 $CD:y=k_1x, EF:y=k_2x, CE:y=k_3(x-a), DF:y=k_4(x+a)$,则过 $C,D,E,F$ 四点的二次曲线系为$$t\left(y-k_1x\right)\left(y-k_2x\right)+\left[y-k_3(x-a)\right]\left[y-k_4(x+a)\right]=0,$$设 $t=t_0$ 时,上式表示相交直线 $CF$ 与 $DE$,令 $y=0$,可知 $x_P,x_Q$ 满足方程\[
\left(t_0k_1k_2+k_3k_4\right)x^2-k_3k_4a^2=0,\]由韦达定理可知 $x_P+x_Q=0$,即 $\left|PM\right|=\left|QM\right|$.
\left(t_0k_1k_2+k_3k_4\right)x^2-k_3k_4a^2=0,\]由韦达定理可知 $x_P+x_Q=0$,即 $\left|PM\right|=\left|QM\right|$.
答案
解析
备注