如图，已知抛物线与 $x$ 轴交于 $A\left(-1,0\right),B\left(4,0\right)$，与 $y$ 轴交于 $C\left(0,-2\right)$．
【难度】
【出处】
无
【标注】
-
$H$ 是 $C$ 关于 $x$ 轴的对称点，$P$ 是抛物线上的一点，当 $\triangle PBH$ 与 $\triangle AOC$ 相似时，求符合条件的 $P$ 点的坐标（求出两点即可）；标注答案点 $P$ 坐标为 $(-1,0)$ 或 $(3,-2)$解析由题意可设抛物线的解析式为 $y=a\left(x+1\right)\left(x-4\right)$，
把点 $C\left(0,-2\right)$ 的坐标代入解析式，可得 $a=\dfrac{1}{2}$，
所以抛物线的解析式为 $y=\dfrac{1}{ 2}x^{2}-\dfrac{3}{ 2}x-2$．
因为 $\triangle AOC$ 是直角三角形，若 $\triangle PBH$ 与 $\triangle AOC$ 相似，则 $\triangle PBH$ 也是直角三角形．
由题意可得点 $H$ 的坐标为 $\left(0,2\right)$，
所以 $AH=\sqrt 5$，$BH=2\sqrt 5$，
从而 $AH^2+BH^2=AB^2$，
所以 $\angle AHB=90^\circ$．
而 $\dfrac{AH}{BH}=\dfrac{AO}{CO}$，
所以 $\triangle AHB\backsim \triangle AOH$，
所以点 $A$ 即为满足条件的点 $P$；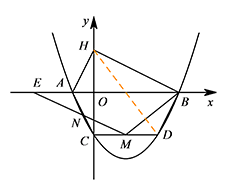
连接 $DH$，同理可证 $\triangle DBH\backsim \triangle AOC$，
所以点 $D$ 也为满足条件的点 $P$．
故符合条件的点 $P$ 坐标为 $(-1,0)$ 或 $(3,-2)$． -
过点 $C$ 作 $CD\parallel AB$，$CD$ 交抛物线于点 $D$，点 $M$ 是线段 $CD$ 上的一动点，作直线 $MN$ 与线段 $AC$ 交于点 $N$，与 $x$ 轴交于点 $E$，且 $\angle BME=\angle BDC$，当 $CN$ 的值最大时，求点 $E$ 的坐标．标注答案点 $E$ 的坐标为 $\left(-\dfrac{17}{ 6},0\right)$解析由抛物线的轴对称性可得 $\angle MCN=\angle BDM=\angle BMN$，$BD=AC=\sqrt 5$，
从而易证 $\triangle MCN\backsim \triangle BDM$，
所以 $\dfrac{MC}{NC}=\dfrac{BD}{MD}$．
令 $MC=m \left(0\leqslant m\leqslant 3\right)$，则 $MD=CD=MC=3-m$，
所以 $\dfrac{m}{NC}=\dfrac{\sqrt 5}{3-m}$，
所以 $NC=-\dfrac{\sqrt 5}5\left(m-\dfrac 32\right)^2+\dfrac{9\sqrt 5}{20}$，
故当 $m=\dfrac 32$ 时，$NC$ 取最大值 $\dfrac{9\sqrt 5}{20}$．
因为 $CM\parallel AE$，
所以 $\dfrac{CM}{AE}=\dfrac{CN}{AN}$，
即 $\dfrac{\dfrac 32}{AE}=\dfrac{\dfrac{9\sqrt 5}{20}}{\sqrt 5-\dfrac{9\sqrt 5}{20}}$，
解得 $AE=\dfrac {11}6$．
所以点 $E$ 的坐标为 $\left(-\dfrac{17}{ 6},0\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
