在正方形 $ABCD$ 中，$BD$ 是一条对角线，点 $P$ 在射线 $CD$ 上（与点 $C,D$ 不重合），连接 $AP$，平移 $\triangle ADP$，使点 $D$ 移动到点 $C$，得到 $\triangle BCQ$，过点 $Q$ 作 $QH \perp BD$ 于 $H$，连接 $AH,PH$．
【难度】
【出处】
无
【标注】
-
如图 1，点 $P$ 在线段 $CD$ 上，判断 $AH$ 与 $PH$ 的数量关系与位置关系并加以证明；标注答案$AH=PH$ 且 $AH\perp PH$解析显然 $\triangle DHQ$ 是等腰直角三角形，
所以 $DH=QH$，$\angle HDP=\angle HQC$．
连接 $CH$．
由题意可得 $DP=QC$，
所以 $\triangle HDP\cong \triangle HQC (\rm{SAS})$，
所以 $PH=CH$，$\angle HPC=\angle HCP$．
由正方形的轴对称性，可得 $HA=HC$，$\angle HAD=\angle HCD$，
所以 $AH=PH$，$\angle HAD=\angle HPC$，
所以 $\angle ADP+\angle AHP=180^\circ$，
从而 $\angle AHP=90^\circ$． -
若点 $P$ 在线段 $CD$ 的延长线上，依题意补全图 2，此时 $(1)$ 问中的结论是否依然成立．标注答案补全图形：
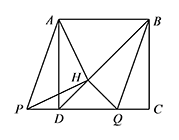此时 $(1)$ 问中结论依然成立解析同样 $\triangle DHQ$ 是等腰直角三角形，
所以 $DH=QH$，$\angle HDP=\angle HQC$．
连接 $CH$．
由题意可得 $DP=QC$，
所以 $\triangle HDP\cong \triangle HQC (\rm{SAS})$，
所以 $PH=CH$，$\angle HPC=\angle HCP$．
由正方形的轴对称性，可得 $HA=HC$，$\angle HAD=\angle HCD$，
所以 $AH=PH$，$\angle HAD=\angle HPD$，
所以 $\angle AHP=\angle ADP=90^\circ$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
