抛物线 $y=ax^2+bx+c$，若 $a,b,c$ 满足 $b=a+c$，则称抛物线 $y=ax^2+bx+c$ 为“恒定”抛物线．而且“恒定”抛物线 $y=ax^2+bx+c$ 必过 $x$ 轴上的一个定点 $A$．已知“恒定”抛物线 $y=\sqrt3x^2-\sqrt3$ 的顶点为 $P$，与 $x$ 轴另一个交点为 $B$，是否存在以 $Q$ 为顶点，与 $x$ 轴另一个交点为 $C$ 的“恒定”抛物线，使得以 $PA,CQ$ 为边的四边形是平行四边形？若存在，求出抛物线解析式；若不存在，请说明理由．
【难度】
【出处】
无
【标注】
【答案】
存在，抛物线的解析式为 $y=-\sqrt3x^2+\sqrt3$ 或 $ y=\sqrt3\left(x+2\right)^2-\sqrt3$
【解析】
令 $y=0$，则 $ax^2+\left(a+c\right)x+c=0$，
解得 $x_1=-\dfrac ca, x_2=-1$，
所以抛物线过 $x$ 轴上的定点 $A\left(-1,0\right)$．
由题意可得点 $B(1,0)$，$P(0,-\sqrt 3)$．
因为以 $PA,CQ$ 为边的四边形是平行四边形，
所以 $PA=CQ$，$PA\parallel CQ$．
过点 $Q$ 作 $QD\perp x$ 轴于点 $D$，则 $AD=CD=AO=1$，$QD=PO=\sqrt 3$．
① 如图，点 $C$ 在点 $A$ 右侧时．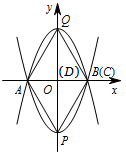
此时 $O,D$ 两点重合，$B,C$ 两点重合．
所以 $C(1,0)$，$Q(0,\sqrt 3)$，
从而得到满足题意的抛物线的解析式为 $ y=-\sqrt3x^2+\sqrt3$．
② 如图，点 $C$ 在点 $A$ 左侧时．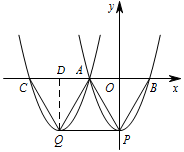
此时 $C(-3,0)$，$Q(-2,-\sqrt 3)$，
可设抛物线解析式为 $y=a(x+2)^2-\sqrt 3$，
将点 $C$ 坐标代入，得 $a(-3+2)^2-\sqrt 3=0$，
解得 $a=\sqrt 3$，
从而得到满足题意的抛物线的解析式为 $y=\sqrt 3(x+2)^2-\sqrt 3$．
综上可得，存在满足题意的抛物线，其解析式为 $y=-\sqrt3x^2+\sqrt3$ 或 $ y=\sqrt3\left(x+2\right)^2-\sqrt3$．
解得 $x_1=-\dfrac ca, x_2=-1$，
所以抛物线过 $x$ 轴上的定点 $A\left(-1,0\right)$．
由题意可得点 $B(1,0)$，$P(0,-\sqrt 3)$．
因为以 $PA,CQ$ 为边的四边形是平行四边形，
所以 $PA=CQ$，$PA\parallel CQ$．
过点 $Q$ 作 $QD\perp x$ 轴于点 $D$，则 $AD=CD=AO=1$，$QD=PO=\sqrt 3$．
① 如图，点 $C$ 在点 $A$ 右侧时．
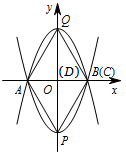此时 $O,D$ 两点重合，$B,C$ 两点重合．所以 $C(1,0)$，$Q(0,\sqrt 3)$，
从而得到满足题意的抛物线的解析式为 $ y=-\sqrt3x^2+\sqrt3$．
② 如图，点 $C$ 在点 $A$ 左侧时．
此时 $C(-3,0)$，$Q(-2,-\sqrt 3)$，可设抛物线解析式为 $y=a(x+2)^2-\sqrt 3$，
将点 $C$ 坐标代入，得 $a(-3+2)^2-\sqrt 3=0$，
解得 $a=\sqrt 3$，
从而得到满足题意的抛物线的解析式为 $y=\sqrt 3(x+2)^2-\sqrt 3$．
综上可得，存在满足题意的抛物线，其解析式为 $y=-\sqrt3x^2+\sqrt3$ 或 $ y=\sqrt3\left(x+2\right)^2-\sqrt3$．
答案
解析
备注
