如图，在同一平面上，两块斜边相等的直角三角板 $\mathrm {Rt}\triangle ABC$ 与 $\mathrm {Rt}\triangle ADC$ 拼在一起，使斜边 $AC$ 完全重合，且顶点 $B,D$ 分别在 $AC$ 的两旁，$\angle ABC=\angle ADC=90^\circ$，$\angle CAD=30^\circ$，$AB=BC=4 {\mathrm {cm}}$．点 $M,N$ 分别从 $A,C$ 点同时以每秒 $1 {\mathrm {cm}}$ 的速度等速出发，且分别在 $AD,CB$ 上沿 $A\to D$，$C \to B$ 的方向运动，当 $N$ 点运动到 $B$ 点时，$M,N$ 两点同时停止运动，取 $DC$ 中点 $P$，连接 $MN,MP,NP$．当 $M,N$ 点运动了 $x$ 秒时，设 $\triangle PMN$ 的面积为 $y$（${\mathrm {cm}}^2$），在整个运动过程中，$\triangle PMN$ 的面积 $y$ 存在最大值，请求出这个最大值．
（参考数据：$\sin 75^\circ = \dfrac{\sqrt 6 + \sqrt 2 }{4}$，$\sin 15^\circ = \dfrac{\sqrt 6 - \sqrt 2 }{4}$）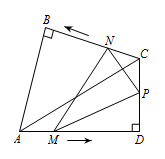
（参考数据：$\sin 75^\circ = \dfrac{\sqrt 6 + \sqrt 2 }{4}$，$\sin 15^\circ = \dfrac{\sqrt 6 - \sqrt 2 }{4}$）
【难度】
【出处】
无
【标注】
【答案】
$\triangle PMN$ 的面积的最大值为 $\dfrac {8\sqrt 3+23\sqrt 6+9\sqrt 2-16}{16}$
【解析】
由题意可得 $AC=4\sqrt 2 \rm{cm}$，$CD=2\sqrt 2 \rm{cm}$，$AD=2\sqrt 6 \rm{cm}$．
如图，过点 $N$ 作 $NE\perp AD$ 于 $E$，作 $NF\perp DC$ 交 $DC$ 延长线于 $F$，则 $NE=DF$．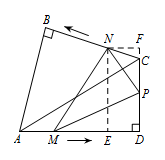
因为 $ \angle ACD=60^\circ $，$\angle ACB=45^\circ $，
所以 $ \angle NCF=75^\circ $，$\angle FNC=15^\circ $，
所以 $ \dfrac{FC}{NC}=\sin 15^\circ=\dfrac{\sqrt 6-\sqrt 2 }{4}$．
又 $NC=x \rm{cm}$，则 $FC=\dfrac{\sqrt 6-\sqrt 2 }{4}x \rm{cm}$，
所以 $NE=DF=\left(\dfrac{\sqrt 6-\sqrt 2 }{4}x + 2\sqrt 2\right)\rm{cm}$．
而 $\dfrac{FN}{NC}=\sin 75^\circ=\dfrac{\sqrt 6 + \sqrt 2 }{4}$，则 $FN=\dfrac{\sqrt 6 + \sqrt 2 }{4}x \rm{cm}$．
所以
$\begin{split} y&=S_{梯形MNFD}-S_{\triangle MDP}-S_{\triangle NFP}\\&= \dfrac{\sqrt 2-\sqrt 6 }{8}{x^2}+\dfrac{7-\sqrt 3-2\sqrt 2}{4}x+2\sqrt 3.\end{split}$
当 $x =-\dfrac{{\dfrac{7 - \sqrt 3 - 2\sqrt 2 }{4}}}{{2 \times \dfrac{\sqrt 2 - \sqrt 6 }{8}}} = \dfrac{7 - \sqrt 3 - 2\sqrt 2 }{\sqrt 6 - \sqrt 2 }$ 时，
$ y_{\max}=\dfrac{6\sqrt 6 + 7\sqrt 3 - 10\sqrt 2 - 30}{4\sqrt 2 - 4\sqrt 6 }=\dfrac {8\sqrt 3+23\sqrt 6+9\sqrt 2-16}{16}$．
故 $\triangle PMN$ 的面积的最大值为 $\dfrac {8\sqrt 3+23\sqrt 6+9\sqrt 2-16}{16}$．
如图，过点 $N$ 作 $NE\perp AD$ 于 $E$，作 $NF\perp DC$ 交 $DC$ 延长线于 $F$，则 $NE=DF$．
因为 $ \angle ACD=60^\circ $，$\angle ACB=45^\circ $，所以 $ \angle NCF=75^\circ $，$\angle FNC=15^\circ $，
所以 $ \dfrac{FC}{NC}=\sin 15^\circ=\dfrac{\sqrt 6-\sqrt 2 }{4}$．
又 $NC=x \rm{cm}$，则 $FC=\dfrac{\sqrt 6-\sqrt 2 }{4}x \rm{cm}$，
所以 $NE=DF=\left(\dfrac{\sqrt 6-\sqrt 2 }{4}x + 2\sqrt 2\right)\rm{cm}$．
而 $\dfrac{FN}{NC}=\sin 75^\circ=\dfrac{\sqrt 6 + \sqrt 2 }{4}$，则 $FN=\dfrac{\sqrt 6 + \sqrt 2 }{4}x \rm{cm}$．
所以
$\begin{split} y&=S_{梯形MNFD}-S_{\triangle MDP}-S_{\triangle NFP}\\&= \dfrac{\sqrt 2-\sqrt 6 }{8}{x^2}+\dfrac{7-\sqrt 3-2\sqrt 2}{4}x+2\sqrt 3.\end{split}$
当 $x =-\dfrac{{\dfrac{7 - \sqrt 3 - 2\sqrt 2 }{4}}}{{2 \times \dfrac{\sqrt 2 - \sqrt 6 }{8}}} = \dfrac{7 - \sqrt 3 - 2\sqrt 2 }{\sqrt 6 - \sqrt 2 }$ 时，
$ y_{\max}=\dfrac{6\sqrt 6 + 7\sqrt 3 - 10\sqrt 2 - 30}{4\sqrt 2 - 4\sqrt 6 }=\dfrac {8\sqrt 3+23\sqrt 6+9\sqrt 2-16}{16}$．
故 $\triangle PMN$ 的面积的最大值为 $\dfrac {8\sqrt 3+23\sqrt 6+9\sqrt 2-16}{16}$．
答案
解析
备注
