五边形 $ABCDE$ 中，$\angle EAB=\angle ABC=\angle BCD=90^\circ$，$AB= BC$，且满足以点 $B$ 为圆心，$AB$ 长为半径的圆弧 $AC$ 与边 $DE$ 相切于点 $F$，连接 $BE,BD$．
【难度】
【出处】
无
【标注】
-
如图 1，求 $\angle EBD $ 的度数；标注答案$\angle EBD=45^\circ$解析连接 $BF$．
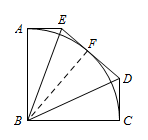$\because BF=BA$，$BE=BE$，$\angle BAE=\angle BFE=90^\circ$，
$\therefore \mathrm {Rt}\triangle BAE\cong \mathrm {Rt}\triangle BFE \mathrm {(HL)}$．
$\therefore\angle ABE=\angle FBE$，
同理可证 $\angle FBD=\angle CBD$，
$\therefore\angle EBF+\angle DBF=45^\circ$，即 $\angle EBD=45^\circ$． -
如图 2，连接 $AC$，分别与 $BE,BD$ 相交于点 $G,H$，若 $AB=1$，$\angle DBC=15^\circ$，求 $AG\cdot HC$ 的值．标注答案$AG\cdot CH=\dfrac{2\sqrt 3}{3}-1$解析$\because\angle DBC=15^\circ$．
$\therefore\angle ABE=90^\circ-15^\circ-45^\circ=30^\circ$．
$\therefore AE=\tan 30^\circ\times 1=\dfrac{\sqrt 3}{3}$．
分别延长 $AE,CD$ 并相交于点 $M$．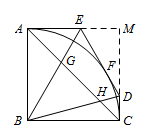
则 $\angle MDE=30^\circ$，$ME=1-\dfrac{\sqrt 3}{3}$，
$\therefore MD=\sqrt 3-1$，
$\therefore CD=1-MD=2-\sqrt 3$．
$\because\angle DBC=15^\circ$，$\angle BCD=90^\circ$，
$\therefore\angle BDC=75^\circ$．
$\because\angle EAG=\angle HCD=45^\circ$，$\angle CDH=75^\circ=\angle AGE$．
$\therefore\triangle AEG\backsim \triangle CHD$，
$\therefore\dfrac{AE}{CH}=\dfrac{AG}{CD}$，
即 $AG\cdot CH=AE\cdot CD=\dfrac{\sqrt 3}{3}\left(2-\sqrt 3\right)=\dfrac{2\sqrt 3}{3}-1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
