如图，已知抛物线 $y=-x^2+bx+c$ 与直线 $AB$ 相较于 $A\left(-3,0\right),B\left(0,3\right)$ 两点．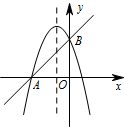
【难度】
【出处】
无
【标注】
-
设 $C$ 是抛物线对称轴上的一动点，求使 $\angle CBA=90^\circ$ 的点 $C$ 的坐标；标注答案点 $C$ 的坐标是 $\left(-1,4\right)$解析把点 $A\left(-3,0\right),B\left(0,3\right)$ 代入 $y=-x^2+bx+c$，
得 $\begin{cases}-9-3b+c=0,\\ c=3.\end{cases}$ 解得 $\begin{cases}b=-2,\\c=3.
\end{cases}$
故所求抛物线的解析式是 $y=-x^2-2x+3$．
过点 $B$ 作 $CB\perp AB$，交抛物线的对称轴于点 $C$，过点 $C$ 作 $CE\perp y$ 轴，垂足为 $E$．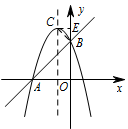
求得抛物线 $y=-x^2-2x+3$ 的对称轴为 $x=-1$，
所以 $ CE=1$，
求得 $\angle ABO=45^\circ$，
所以 $\angle CBE=45^\circ$，
所以 $ BE=CE=1$，
所以 $ OE=OB+BE=4$，
所以 点 $C$ 的坐标是 $\left(-1,4\right)$． -
探究在抛物线上是否存在点 $P$，使得 $\triangle APB$ 的面积等于 $3$，若存在，求点 $P$ 的坐标．标注答案点 $P$ 的坐标分别为 $P_1\left(-1,4\right)$，$P_2\left(-1,3\right)$，$P_3\left(\dfrac{-3+\sqrt{17}}{2},\dfrac{-1+\sqrt{17}}{2}\right)$，$P_4\left(\dfrac{-3-\sqrt{17}}{2},\dfrac{-1-\sqrt{17}}{2}\right)$解析假设在抛物线上存在符合要求的点 $P$，分别连接 $PA,PB$，过 $P$ 作 $PD\perp AB$ 于点 $D$，作 $PF\parallel y$ 轴交 $AB$ 于点 $F$．
在 $\mathrm {Rt}\triangle ABO$ 中，求得 $AB=3\sqrt2$，
因为 $S_{\triangle APB}=3$，
所以 $ PD=\sqrt2$．
因为 $ \angle PFD=\angle ABO=45^\circ$，
所以 $ PF=2$．
设点 $P$ 的坐标为 $\left(m,-m^2-2m+3\right)$．
求得直线 $AB$ 的解析式为 $y=x+3$，则点 $F$ 的坐标为 $\left(m,m+3\right)$．
① 当点 $P$ 在直线 $AB$ 上方时，可得 $-m^2-2m+3=m+3+2$，
解得 $m_1=-1, m_2=-2$，
所以符合要求的点 $P$ 的坐标为 $P_1\left(-1,4\right)$，$P_2\left(-2,3\right)$；
② 当点 $P$ 在直线 $AB$ 下方时，可得 $-m^2-2m+3=m+3-2$，
解得 $m_1=\dfrac{-3+\sqrt{17}}{2}, m_2=\dfrac{-3-\sqrt{17}}{2}$，
所以符合要求的点 $P$ 的坐标为 $P_3\left(\dfrac{-3+\sqrt{17}}{2},\dfrac{-1+\sqrt{17}}{2}\right)$，$P_4\left(\dfrac{-3-\sqrt{17}}{2},\dfrac{-1-\sqrt{17}}{2}\right)$．
综上可得，符合要求的点 $P$ 有四个，点 $P$ 的坐标分别为 $P_1\left(-1,4\right)$，$P_2\left(-1,3\right)$，$P_3\left(\dfrac{-3+\sqrt{17}}{2},\dfrac{-1+\sqrt{17}}{2}\right)$，$P_4\left(\dfrac{-3-\sqrt{17}}{2},\dfrac{-1-\sqrt{17}}{2}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
