如图，抛物线 $y = a{x^2} + bx + c\left(a\neq 0\right)$ 与 $x$ 轴交于 $A\left(-4,0\right),B\left(2,0\right)$，与 $y$ 轴交与点 $C\left(0,2\right)$．
【难度】
【出处】
无
【标注】
-
若点 $D$ 为该抛物线上的一个动点，且在直线 $AC$ 上方，当以 $A,C,D$ 为顶点的三角形面积最大时，求点 $D$ 的坐标及此时三角形的面积；标注答案点 $D$ 坐标为 $\left(-2,2\right)$ 时，$\triangle ACD$ 的面积取最大值，最大值为 $2$解析设抛物线的解析式为 $y = a{x^2} + bx + c\left(a \ne 0\right)$．
因为 抛物线过点 $A\left(-4,0\right)$，$B\left(2,0\right)$，$C\left(0,2\right)$．
所以 $\begin{cases}16a - 4b + c = 0, \\ 4a + 2b + c = 0, \\ c = 2 ,\end{cases}$ 解得 ${\begin{cases} a = - \dfrac{1}{4} ,\\ b = - \dfrac{1}{2}, \\ c = 2 ,\end{cases}}$
所以抛物线的解析式为 $y = - \dfrac{1}{4}{x^2} - \dfrac{1}{2}x + 2$．
设直线 $AC$ 的解析式为 $y = {k_1}x + {b_1}\left({k_1} \ne 0\right)$．
因为 $ y = {k_1}x + {b_1}$ 过点 $A\left(-4,0\right)$，$C\left(0,2\right)$．
所以 $\begin{cases}-4{k_1}+{b_1}=0,\\{b_1}=2,\end{cases}$ 解得 $\begin{cases}{k_1}=\dfrac{1}{2},\\{b_1}=2. \end{cases}$
所以直线 $AC$ 的解析式为 $y=\dfrac{1}{2}x + 2$．
可设点 $D$ 的坐标为 $\left(x,- \dfrac{1}{4}{x^2}-\dfrac{1}{2}x+2\right)$，则点 $T$ 的坐标为 $\left(x,\dfrac{1}{2}x+2\right)$．
所以 $DT=-\dfrac{1}{4}{x^2} - \dfrac{1}{2}x + 2 - \dfrac{1}{2}x - 2=- \dfrac{1}{4}{x^2} - x$，
如图，过点 $D$ 作 $AC,AB$ 的垂线，垂足分别为点 $F,G$，$DG$ 交 $AC$ 于点 $T$．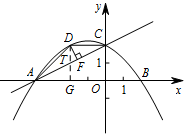
所以 $\triangle DFT\backsim \triangle AOC$，
所以 $\dfrac{DF}{AO} = \dfrac{DT}{AC}$．
在 $\mathrm {Rt}\triangle AOC$ 中，$AC=\sqrt {O{A^2} + O{C^2}} = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 $．
所以 $ DF=\dfrac{DT \cdot AO}{AC}=\dfrac{{4\left(- \dfrac{1}{4}{x^2} - x\right)}}{2\sqrt 5 }=\dfrac{\sqrt 5 }{5}\left(- \dfrac{1}{2}{x^2} - 2x\right)$，
$\begin{split}{S_{\triangle ACD}} &= \dfrac{1}{2}AC \cdot DF \\&= \dfrac{1}{2} \cdot 2\sqrt 5 \cdot \dfrac{\sqrt 5 }{5}\left(- \dfrac{1}{2}{x^2} - 2x\right)
\\&= - \dfrac{1}{2}{x^2} - 2x\\&= - \dfrac{1}{2}\left({x^2} + 4x\right)\\&= - \dfrac{1}{2}{\left(x + 2\right)^2} + 2,\end{split}$
故当 $x=-2$，即点 $D$ 坐标为 $\left(-2,2\right)$ 时，$\triangle ACD$ 的面积取最大值，最大值为 $2$． -
以 $AB$ 为直径作 $\odot M$，直线经过点 $E\left(-1,-5\right)$，并且与 $\odot M$ 相切，求该直线的解析式．标注答案$y=-\dfrac{4}{3}x-\dfrac{19}{3}$ 或 $y=\dfrac{4}{3}x-\dfrac{11}{3}$解析如图，过 $E$ 点作 $\odot M$ 的切线，切点为 $P$，这样的切线共有 $2$ 条．
连接 $MP,ME$，过点 $P$ 作 $PH\perp x$ 轴于点 $H$．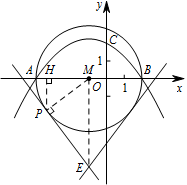
因为 $ A\left(-4,0\right)$，$B\left(2,0\right)$，
所以 $ M\left(-1,0\right)$，$\odot M$ 的半径 $MP=MA=3$．
又 $M\left(-1,0\right)$，$E\left(-1,-5\right)$
所以 $ ME=5$，
所以在 $\mathrm {Rt}\triangle MPE$ 中，$PE=4$．
显然 $\angle HMP=\angle PEM$，即 $\sin\angle HMP=\sin\angle PEM$，
所以 $ \dfrac{PH}{PM}=\dfrac{MP}{ME}$，从而 $PH=\dfrac{PM^2}{ME}=\dfrac 95$．
所以 $ MH=\sqrt{PM^2-PH^2}=\dfrac{12}5$．
所以点 $P$ 的坐标为 $\left( - \dfrac{17}{5}, - \dfrac{9}{5}\right)$．
设直线 $PE$ 的解析式为 $y={k_2}x+{b_2} \left({k_2}\ne 0\right)$，
所以 $ {\begin{cases}-\dfrac{17}{5}{k_2}+{b_2}=-\dfrac{9}{5},\\-{k_2}+{b_2}=-5,\end{cases}}$
解得 ${\begin{cases}{k_2}=-\dfrac{4}{3}, \\ {b_2}=-\dfrac{19}{3}, \end{cases}}$
所以直线 $PE$ 的解析式为 $y=-\dfrac{4}{3}x-\dfrac{19}{3}$．
同理，可求得另一条切线的解析式为 $y=\dfrac{4}{3}x-\dfrac{11}{3}$，
综上所述，满足题意的直线的解析式为 $y=-\dfrac{4}{3}x-\dfrac{19}{3}$ 或 $y=\dfrac{4}{3}x-\dfrac{11}{3}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
