如图，二次函数 $y=ax^2+bx+3$ 的图象与 $x$ 轴相交于点 $A\left(- 3,0\right),B\left(1,0\right)$，与 $y$ 轴相交于点 $C$，点 $G$ 是二次函数图象的顶点，直线 $GC$ 交 $x$ 轴于点 $H\left(3,0\right)$，$AD$ 平行 $GC$ 交 $y$ 轴于点 $D$．如图，点 $M\left(t,p\right)$ 是该二次函数图象上的动点，并且点 $M$ 在第二象限内，过点 $M$ 的直线 $y=kx$ 交二次函数的图象于另一点 $N$．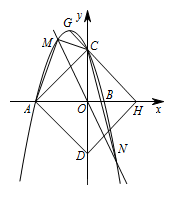
【难度】
【出处】
无
【标注】
-
若四边形 $ADCM$ 的面积为 $S$，请求出 $S$ 关于 $t$ 的函数表达式，并写出 $t$ 的取值范围；标注答案$ S_{ 四边形ADCM}=-\dfrac 32t^2-\dfrac 92t+9 (-3<t<0) $解析因为二次函数 $y=ax^2+bx+3$ 过点 $A\left(-3, 0\right),B\left(1, 0\right)$，
所以 $\begin{cases}9a-3b+3=0,\\ a+b+3=0,\end{cases}$ 解得 $\begin{cases}a=-1,\\ b=-2.\end{cases}$
所以二次函数的表达式为 $y=-x^2-2x+3=-(x+1)^2+4$．
所以点 $C$ 的坐标为 $(0,3)$，点 $G$ 的坐标为 $(-1,4)$，
从而直线 $GC$ 的解析式为 $y=-x+3$，
所以点 $H$ 的坐标为 $(3,0)$，即 $OH=OC=3$．
由 $AD\parallel CH$，可得 $OA=OD=3$．
可设点 $M$ 的坐标为 $\left(t,-t^2-2t+3\right)$，且 $-3<t<0$．
作 $MK\perp x$ 轴于点 $K$，作 $ME\perp y$ 轴于点 $E$．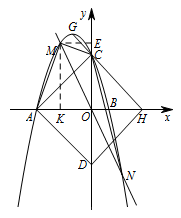
则 $MK=-t^2-2t+3$，$ME={\left|{t}\right|}=-t$．
所以 $\begin{split} S_{四边形AOCM}&=\dfrac 12\times 3\left(-t^ 2-2 t +3\right)+ \dfrac 12\times 3\times \left(-t\right)\\ &=-\dfrac 32t^2-\dfrac 92t+\dfrac 92.\end{split}$
而 $S_{\triangle AOD}=\dfrac 12\times 3\times 3=\dfrac 92$．
所以
$ S_{ 四边形ADCM}=S_{四边形AOCM} + S_{\triangle AOD}=-\dfrac 32t^2-\dfrac 92t+9 (-3<t<0) .$ -
若 $\triangle CMN$ 的面积等于 $\dfrac{21}{4}$，请求出此时 $(1)$ 中 $S$ 的值．标注答案$S $ 的值是 $12 $ 或 $S= \dfrac{99}{8}$解析设点 $ N$ 的坐标为 $\left(t_1,p_1\right)$，过点 $ N$ 作 $ NF\perp y$ 轴于点 $ F$．
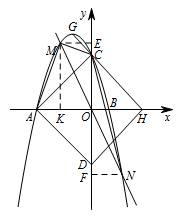所以 $ NF={\left|{t_1}\right|}$．
又由 $(1)$ 知 $ME= t$，则 $S_{\triangle CMN}= S_{\triangle COM} + S_{\triangle CON}= \dfrac 1 2 OC\cdot \left({\left|{ t}\right|} + t_1 \right)$．
又点 $ M\left(t, p\right)$，$ N\left(t _1, p_1\right)$ 分别在第二、四象限内，
所以 $t<0$，$t_1>0$，
所以 $S_{\triangle CMN}= \dfrac 32\left(t_1- t\right)$，即 $ \dfrac 32\left( t_1- t\right)=\dfrac{21}{4}$，
所以 $ t _1- t =\dfrac 72$．
由直线 $ y=kx $ 交二次函数的图象于点 $ M$，$ N $
得 $\begin{cases}y=kx,\\ y=-x^2-2x+3,\end{cases}$
则 $ x^2+\left(2+k\right)x-3=0 $．
所以 $ x=\dfrac{-\left(2+k\right)\pm\sqrt{\left(2+k\right)^2-4\times 1\times\left(-3\right)}}{2}$，
即 $t =\dfrac{-\left(2+k\right)-\sqrt{\left(2+k\right)^2-4\times 1\times\left(-3\right)}}{2}$，
$t_1=\dfrac{-\left(2+k\right)+\sqrt{\left(2+k\right)^2-4\times 1\times\left(-3\right)}}{2}$，
所以 $ t_1- t= \sqrt{\left(2 + k\right)^2 +12} =\dfrac 72$，
所以 $ \left(2+ k\right)^2+12=\dfrac{49}{4}$，
解得 $k_1=-\dfrac 32$，$ k_2=-\dfrac 52$．
又 $\left(k+2\right)^2+12$ 恒大于 $0$，且 $k<0$．
所以 $ k_1=-\dfrac 32$，$k_2=-\dfrac 52$ 符合条件．
① 若 $ k=-\dfrac 32$，有 $ x^2+\left(2-\dfrac 32\right)x-3=0$，
解得 $ x_1=-2$，$ x_2=\dfrac32$（不符合题意，舍去）．
② 若 $k=-\dfrac 52$，有 $ x^2+\left(2-\dfrac 52\right)x-3=0$，
解得 $x_3=-\dfrac 32$，$x_4=2$（不符合题意，舍去）．
所以 $t =-2 $ 或 $-\dfrac 32$．
当 $ t =-2$ 时，$S=12$；
当 $t =-\dfrac 32$ 时，$S= \dfrac{99}{8}$．
所以 $S $ 的值是 $12 $ 或 $S= \dfrac{99}{8}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
