如图，四边形 $OABC$ 是矩形，点 $A,C$ 在坐标轴上，$\triangle ODE$ 是由 $\triangle OCB$ 绕点 $O$ 顺时针旋转 $90^\circ$ 得到的，点 $D$ 在 $x$ 轴上，直线 $BD$ 交 $y$ 轴于点 $F$，交 $OE$ 于点 $H$，线段 $BC,OC$ 的长是方程 $x^2-6x+8=0$ 的两个根，且 $OC>BC$．点 $M$ 在坐标轴上，平面内是否存在点 $N$，使以点 $D,F,M,N$ 为顶点的四边形是矩形？若存在，请求出点 $N$ 的坐标；若不存在，请说明理由．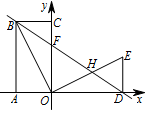
【难度】
【出处】
无
【标注】
【答案】
存在，点 $N$ 的坐标为 $\left(\dfrac {20}{9},-\dfrac 83\right)$，$\left(-4,-\dfrac {10}{3}\right)$ 或 $\left(4,\dfrac 83\right)$
【解析】
解方程 $x^2-6x+8=0$，得 $x_1=2, x_2=4$．
因为 $OC>BC$，所以 $ OD=OC=4$，$BC=2$，
所以点 $B\left(-2,4\right)$，点 $D\left(4,0\right)$．
所以直线 $BD$ 的解析式为 $y=-\dfrac 23x+\dfrac 83$．
所以点 $F\left(0,\dfrac 83\right)$．
因为以点 $D,F,M,N$ 为顶点的四边形是矩形，
所以 $\triangle DFM$ 为直角三角形．
① 当 $\angle MFD=90^\circ$ 时，则 $M$ 只能在 $x$ 轴上，连接 $FN$ 交 $MD$ 于点 $G$，如图．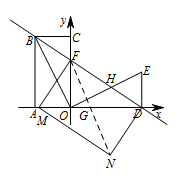
则有 $\triangle MOF\backsim \triangle FOD$，所以 $ \dfrac {OM}{OF}=\dfrac {OF}{OD}$，
即 $\dfrac {OM}{\dfrac 83}=\dfrac {\dfrac 83}{4}$，解得 $OM=\dfrac {16}{9}$．
所以点 $M\left(-\dfrac {16}{9},0\right)$，点 $G\left(\dfrac {10}{9},0\right)$．
设 $N$ 点坐标为 $\left(x,y\right)$，则 $\dfrac {x+0}{2}=\dfrac {10}{9}$，$\dfrac {y+\dfrac 83}{2}=0$，
解得 $x=\dfrac {20}{9}$，$y=-\dfrac 83$，
此时 $N$ 点坐标为 $\left(\dfrac {20}{9},-\dfrac 83\right)$．
② 当 $\angle MDF=90^\circ$ 时，则 $M$ 只能在 $y$ 轴上，连接 $DN$ 交 $MF$ 于点 $G$，如图．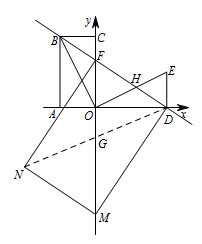
则有 $\triangle FOD\backsim \triangle DOM$，所以 $ \dfrac {OF}{OD}=\dfrac {OD}{OM}$，
即 $\dfrac {\dfrac 83}{4}=\dfrac {4}{OM}$，解得 $OM=6$，
所以点 $M\left(0,-6\right)$，点 $G\left(0,-\dfrac 53\right)$．
设 $N$ 点坐标为 $\left(x,y\right)$，则 $\dfrac {x+4}{2}=0$，$\dfrac {y+0}{2}=-\dfrac 53$，
解得 $x=-4$，$y=-\dfrac {10}{3}$，
此时 $N$ 点坐标为 $\left(-4,-\dfrac {10}{3}\right)$．
③ 当 $\angle FMD=90^\circ$ 时，则可知 $M$ 为原点，如图．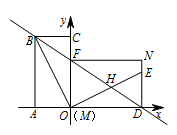
因为四边形 $MFND$ 为矩形，
所以 $NF=OD=4$，$ND=OF=\dfrac 83$，
可求得 $N$ 点坐标为 $\left(4,\dfrac 83\right)$．
综上所述，$N$ 点坐标为 $\left(\dfrac {20}{9},-\dfrac 83\right)$ 或 $\left(-4,-\dfrac {10}{3}\right)$ 或 $\left(4,\dfrac 83\right)$．
因为 $OC>BC$，所以 $ OD=OC=4$，$BC=2$，
所以点 $B\left(-2,4\right)$，点 $D\left(4,0\right)$．
所以直线 $BD$ 的解析式为 $y=-\dfrac 23x+\dfrac 83$．
所以点 $F\left(0,\dfrac 83\right)$．
因为以点 $D,F,M,N$ 为顶点的四边形是矩形，
所以 $\triangle DFM$ 为直角三角形．
① 当 $\angle MFD=90^\circ$ 时，则 $M$ 只能在 $x$ 轴上，连接 $FN$ 交 $MD$ 于点 $G$，如图．
则有 $\triangle MOF\backsim \triangle FOD$，所以 $ \dfrac {OM}{OF}=\dfrac {OF}{OD}$，即 $\dfrac {OM}{\dfrac 83}=\dfrac {\dfrac 83}{4}$，解得 $OM=\dfrac {16}{9}$．
所以点 $M\left(-\dfrac {16}{9},0\right)$，点 $G\left(\dfrac {10}{9},0\right)$．
设 $N$ 点坐标为 $\left(x,y\right)$，则 $\dfrac {x+0}{2}=\dfrac {10}{9}$，$\dfrac {y+\dfrac 83}{2}=0$，
解得 $x=\dfrac {20}{9}$，$y=-\dfrac 83$，
此时 $N$ 点坐标为 $\left(\dfrac {20}{9},-\dfrac 83\right)$．
② 当 $\angle MDF=90^\circ$ 时，则 $M$ 只能在 $y$ 轴上，连接 $DN$ 交 $MF$ 于点 $G$，如图．
则有 $\triangle FOD\backsim \triangle DOM$，所以 $ \dfrac {OF}{OD}=\dfrac {OD}{OM}$，即 $\dfrac {\dfrac 83}{4}=\dfrac {4}{OM}$，解得 $OM=6$，
所以点 $M\left(0,-6\right)$，点 $G\left(0,-\dfrac 53\right)$．
设 $N$ 点坐标为 $\left(x,y\right)$，则 $\dfrac {x+4}{2}=0$，$\dfrac {y+0}{2}=-\dfrac 53$，
解得 $x=-4$，$y=-\dfrac {10}{3}$，
此时 $N$ 点坐标为 $\left(-4,-\dfrac {10}{3}\right)$．
③ 当 $\angle FMD=90^\circ$ 时，则可知 $M$ 为原点，如图．
因为四边形 $MFND$ 为矩形，所以 $NF=OD=4$，$ND=OF=\dfrac 83$，
可求得 $N$ 点坐标为 $\left(4,\dfrac 83\right)$．
综上所述，$N$ 点坐标为 $\left(\dfrac {20}{9},-\dfrac 83\right)$ 或 $\left(-4,-\dfrac {10}{3}\right)$ 或 $\left(4,\dfrac 83\right)$．
答案
解析
备注
