矩形 $AOCD$ 绕顶点 $A(0,5)$ 逆时针方向旋转，当旋转到如图所示的位置时，边 $BE$ 交边 $CD$ 于 $M$，且 $ME=2$，$CM=4$．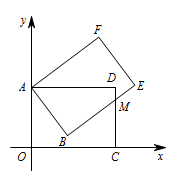
【难度】
【出处】
无
【标注】
-
求 $AD$ 的长；标注答案$AD=7$解析如图，延长 $CD$ 交 $EF$ 于点 $G$，连接 $AG$．
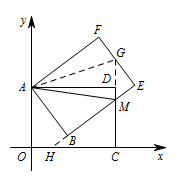由旋转的性质得 $AF=AD$，$EF=CD=AB=5$，$BE=OC$，$\angle F=\angle ADC=\angle ADG=90^\circ$，
所以 $\mathrm{Rt}\triangle ADG\cong \mathrm{Rt}\triangle AFG (\mathrm{HL})$，
所以 $DG=FG$．
令 $FG=x$，则 $EG=5-x$．
在 $\mathrm{Rt}\triangle MEG$ 中，有 $2^2+(5-x)^2=(x+1)^2$，
解得 $x=\dfrac 73$，
从而 $EG=\dfrac 83$，$MG=\dfrac{10}3$．
延长 $MB$ 交 $OC$ 于点 $H$，同理可得 $OH=BH$．
易证 $\triangle MEG\backsim \triangle MCH$，
所以 $\dfrac{MG}{MH}=\dfrac{EG}{CH}=\dfrac{ME}{MC}=\dfrac 12$，
从而 $MH=\dfrac{20}3$，$CH=\dfrac{16}3$．
由 $BE=OC$，可得 $OH+HC=EH-BH$，
即 $OH+\dfrac{16}3=\dfrac{20}3+2-OH$，解得 $OH=\dfrac 53$．
所以 $AD=OC=\dfrac 53+\dfrac{16}3=7$． -
在经过 $A,B,D$ 三点的抛物线上是否存在点 $P$，使 $S_{\triangle PAM}=\dfrac{25}{2}$？若存在，求出 $P$ 点坐标；若不存在，请说明理由．标注答案存在，满足条件的点 $P$，其坐标为 $(3,1)$，$\left(\dfrac{25}{7},\dfrac{45}{49}\right)$，$\left(\dfrac{23-2\sqrt{386}}{7},\dfrac{397+2\sqrt{386}}{49}\right) $ 或 $ \left(\dfrac{23+2\sqrt{386}}{7},\dfrac{397-2\sqrt{386}}{49}\right)$解析过点 $B$ 作 $BK\perp OC$ 于点 $K$．
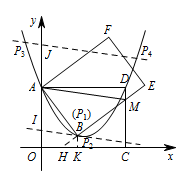则 $\dfrac{HK}{HC}=\dfrac{BK}{MC}=\dfrac{HB}{HM}=\dfrac 14$，
所以 $HK=\dfrac 43$，$BK=1$，
所以点 $B$ 的坐标为 $(3,1)$．
从而过点 $A,B,D$ 的抛物线的解析式为 $y=\dfrac 13x^2-\dfrac 73x+5$．
由 $S_{\triangle ABM}=S_{梯形AOCM}-S_{梯形AOKB}-S_{梯形MCKB}=\dfrac{25}2$，
所以点 $P_1(3,1)$ 为满足条件的一个点 $P$；
由 $A(0,5),M(7,4)$，可得直线 $AM$ 的解析式为 $y=-\dfrac 17x+5$．
过点 $B$ 作 $BI\parallel AM$，交 $y$ 轴于点 $I$，
则可设直线 $BI$ 的解析式为 $y=-\dfrac 17x+b_1$，
将点 $B(3,1)$ 坐标代入，可得 $b_1=\dfrac{10}7$，
从而直线 $BI$ 的解析式为 $y=-\dfrac 17x+\dfrac{10}7$．
联立方程组 $\begin{cases}y=\dfrac 13x^2-\dfrac 73x+5,\\ y=-\dfrac 17x+\dfrac{10}7,\end{cases}$
解得 $\begin{cases}x_1=3,\\ y_1=1,\end{cases}\begin{cases}x_2=\dfrac{25}{7},\\ y_2=\dfrac{45}{49}.\end{cases}$
所以点 $P_2\left(\dfrac{25}{7},\dfrac{45}{49}\right)$ 为满足条件的一个点 $P$；
由直线 $BI$ 解析式可得点 $I$ 坐标为 $\left(0,\dfrac{10}7\right)$．
作点 $J$ 与点 $I$ 关于点 $A$ 成中心对称，则点 $J$ 的坐标为 $\left(0,\dfrac{60}7\right)$，
从而过点 $J$ 且与直线 $AM$ 平行的直线的解析式为 $y=-\dfrac 17x+\dfrac{60}7$．
联立方程组 $\begin{cases}y=\dfrac13x^2-\dfrac 73x+5,\\y=-\dfrac 17x+\dfrac{60}{7}.\end{cases}$
解得 $\begin{cases}x_1=\dfrac{23-2\sqrt{386}}{7},\\ y_1=\dfrac{397+2\sqrt{386}}{49},\end{cases}\begin{cases}x_2=\dfrac{23+2\sqrt{386}}{7},\\ y_2=\dfrac{397-2\sqrt{386}}{49}.\end{cases}$
此时点 $P$ 的坐标为 $P_3\left(\dfrac{23-2\sqrt{386}}{7},\dfrac{397+2\sqrt{386}}{49}\right)$，$P_4\left(\dfrac{23+2\sqrt{386}}{7},\dfrac{397-2\sqrt{386}}{49}\right)$．
综上可得，存在满足条件的点 $P$，其坐标为 $(3,1)$，$\left(\dfrac{25}{7},\dfrac{45}{49}\right)$，$\left(\dfrac{23-2\sqrt{386}}{7},\dfrac{397+2\sqrt{386}}{49}\right) $ 或 $ \left(\dfrac{23+2\sqrt{386}}{7},\dfrac{397-2\sqrt{386}}{49}\right)$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
