已知 $\angle MAN=135^\circ$，正方形 $ABCD$ 绕点 $A$ 旋转．当正方形 $ABCD$ 旋转到 $\angle MAN$ 的外部（顶点 $A$ 除外）时，$AM,AN$ 分别与正方形 $ABCD$ 的边 $CB,CD$ 的延长线交于点 $M,N$，连接 $MN$．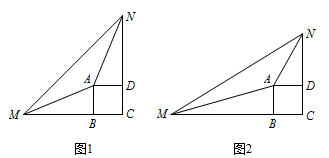
【难度】
【出处】
无
【标注】
-
如图 1，若 $BM=DN$，则线段 $MN$ 与 $BM+DN$ 之间的数量关系是
$\therefore AN=AM$，$ \angle 1=\angle 2=67.5^\circ $．
过点 $A$ 作 $AE\perp MN$ 交 $MN$ 于点 $E$．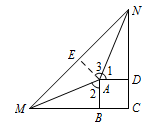
则有 $EN=EM$．
又 $\angle 3=\angle 1=67.5^\circ$，
$\therefore \triangle ADN\cong\triangle AEN$．
$\therefore DN=EN$．
同理 $MB=ME$．
$\therefore MN=BM+DN$． -
如图 2，若 $BM\neq DN$，请判断 $(1)$ 中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；标注答案如图，若 $BM\neq DN$，$(1)$ 中的数量关系仍成立．理由如下：
延长 $NC$ 到点 $P$，使 $DP=BM$，连接 $AP$．
$\because $ 四边形 $ABCD$ 是正方形，
$\therefore AB=AD$，$\angle ABM=\angle ADC=90^\circ $．
$\therefore \triangle ABM\cong \triangle ADP ({\mathrm {SAS}})$，
$\therefore AM=AP$，$\angle 1=\angle 2=\angle 3$．
$\because \angle 1+\angle 4=90^\circ $，
$\therefore \angle 3+\angle 4=90^\circ $．
$\because \angle MAN=135^\circ $，
$\therefore \angle PAN=360^\circ -\angle MAN-\left(\angle 3+\angle 4\right)=360^\circ -135^\circ -90^\circ =135^\circ $．
$\therefore \triangle ANM\cong \triangle ANP ({\mathrm {SAS}})$，
$\therefore MN=PN$．
$\because PN=DP+DN=BM+DN$，
$\therefore MN=BM+DN$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
