已知抛物线经过 $A\left(-3,0\right),B\left(1,0\right),C\left(2,\dfrac 52\right)$ 三点,其对称轴交 $x$ 轴于点 $H$,一次函数 $y=kx+b\left(k\neq 0\right)$ 的图象经过点 $C$,与抛物线交于另一点 $D$(点 $D$ 在点 $C$ 的左边),与抛物线的对称轴交于点 $E$.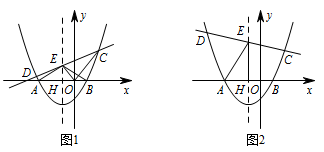
【难度】
【出处】
无
【标注】
-
如图 1,当 $S_{\triangle EOC}=S_{\triangle EAB}$ 时,求一次函数的解析式;标注答案一次函数的解析式为 $y= \dfrac {5}{12}x+\dfrac 53$解析设抛物线的解析式为 $y=ax^2+bx+c$,
因为抛物线经过 $A\left(-3,0\right),B\left(1,0\right),C\left(2,\dfrac 52 \right)$ 三点,
所以 $\begin{cases} 9a-3b+c=0, \\ a+b+c=0, \\ 4a+2b+c=\dfrac 52,\end{cases}$ 解得 $\begin{cases} a=\dfrac 12, \\ b=1, \\ c=-\dfrac 32,\end{cases}$
所以抛物线的解析式为 $y= \dfrac 12x^2+x-\dfrac 32$.
如图,记直线 $CD$ 交 $y$ 轴于点 $F$.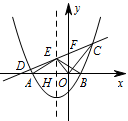 将 $C$ 点坐标代入直线 $CD$,得 $2k+b=\dfrac 52. \quad \cdots \cdots ① $
将 $C$ 点坐标代入直线 $CD$,得 $2k+b=\dfrac 52. \quad \cdots \cdots ① $
当 $x=0$ 时,$y=b$,即 $F\left(0,b\right)$.
当 $x=-1$ 时,$y=-k+b$,即 $E\left(-1,-k+b\right)$.
当 $S_{\triangle EOC}=S_{\triangle EAB}$ 时,
得 $\dfrac 12\times \left[2-\left(-1\right)\right]b=\dfrac12 \left[1-\left(-3\right)\right]\left(-k+b\right) . \quad \cdots \cdots ② $
联立方程 $ ①② $,
得 $\begin{cases} 2k+b=\dfrac 52,\\ \dfrac 12\times \left[2-\left(-1\right)\right]b=\dfrac12 \left[1-\left(-3\right)\right]\left(-k+b\right),\end{cases}$ 解得 $\begin{cases} k=\dfrac {5}{12}, \\ b=\dfrac 53.\end{cases}$
所以当 $S_{\triangle EOC}=S_{\triangle EAB}$ 时,一次函数的解析式为 $y= \dfrac {5}{12}x+\dfrac 53$. -
如图 2,设 $\angle CEH=\alpha$,$\angle EAH=\beta$,当 $\alpha>\beta$ 时,直接写出 $ k $ 的取值范围.标注答案$k$ 的取值范围是 $-\dfrac 12<k<\dfrac 56$ 或 $ \dfrac56<k<\dfrac43 $解析如图所示,
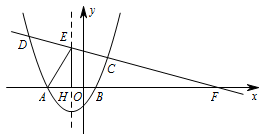 设 $CD$ 的解析式为 $y=kx+\dfrac 52 -2k$,
设 $CD$ 的解析式为 $y=kx+\dfrac 52 -2k$,
当 $y=0$ 时,$kx+\dfrac 52 -2k=0$,
解得 $x=2-\dfrac {5}{2k}$,
所以 $F\left(2-\dfrac {5}{2k},0\right)$,$FH=\left|3-\dfrac {5}{2k}\right|$.
当 $x=-1$ 时,$y= \dfrac 52-3k$,
所以 $E\left(-1, \dfrac 52-3k\right)$,$AH=-1-\left(-3\right)=2$.
当 $\alpha>\beta$ 时,$\tan \alpha>\tan \beta$,即 $\dfrac {FH}{EH}>\dfrac {EH}{AH} $,
所以 $\dfrac{\left|3-\dfrac{5}{2k}\right|}{\left|\dfrac 52-3k\right|}>\dfrac{\left|\dfrac 52-3k\right|}{2} \left(k\ne\dfrac56\right)$.
当 $k\ne0$ 时,上式变形为 $\dfrac{\left|6k-5\right|}{\left|5k-6k^2\right|}>\dfrac{\left|5-6k\right|}{4} $,
所以 $\left|5k-6k^2\right|<4$,所以 $\begin{cases}6k^2-5k+4>0,\\ 6k^2-5k-4<0 .\end{cases}$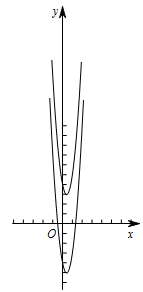 结合图象,可得不等式组的解集为 $-\dfrac12<k<\dfrac43 \left(k\ne0,k\ne\dfrac56\right)$.
结合图象,可得不等式组的解集为 $-\dfrac12<k<\dfrac43 \left(k\ne0,k\ne\dfrac56\right)$.
综上可得,$k$ 的取值范围是 $-\dfrac 12<k<\dfrac 56$ 或 $ \dfrac56<k<\dfrac43 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2