如图,$B\left(2m,0\right)$,$C\left(3m,0\right)$ 是平面直角坐标系中两点,其中 $m$ 为常数,且 $m>0$,$E\left(0,n\right)$ 为 $y$ 轴上一动点.以 $BC$ 为边在 $x$ 轴上方作矩形 $ABCD$,使 $AB=2BC$,画射线 $OA$.把 $\triangle ADC$ 绕点 $C$ 逆时针旋转 $90^\circ$ 得 $\triangle A'D'C'$,连接 $ED'$.抛物线 $y=ax^2+bx+n (a\neq 0)$ 过 $E,A'$ 两点.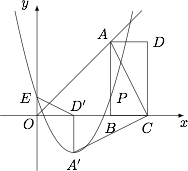

【难度】
【出处】
无
【标注】
-
当抛物线的顶点为 $A'$,抛物线与线段 $AB$ 交于点 $P$,且 $\dfrac{BP}{AP}=\dfrac 13$ 时,$\triangle D'OE$ 与 $\triangle ABC$ 是否相似?说明理由;标注答案$\triangle D'OE\backsim \triangle ABC$解析由旋转的性质,可得 $A'D'=AD=m$,$CD'=CD=2m$,
所以点 $A'$ 的坐标为 $(m,-m)$.
因为点 $A'$ 为抛物线的顶点,
所以可设抛物线的解析式为 $y=a\left(x-m\right)^2-m$.
由已知可得 $A\left(2m,2m\right)$,$B\left(2m,0\right)$.
因为 $\dfrac {BP}{AP}=\dfrac 13$,
所以点 $P$ 的坐标为 $\left(2m,\dfrac 12m\right)$.
因为抛物线过点 $P$,
所以 $\dfrac 12m=a\left(2m-m\right)^2-m$,整理得 $am=\dfrac 32$.
因为抛物线过点 $E\left(0,n\right)$,
所以 $n=a\left(0-m\right)^2-m=m(am-1)=\dfrac 12m$.
所以 $\dfrac{OE}{OD'}=\dfrac nm=\dfrac 12=\dfrac{BC}{AB}$.
又因为 $\angle EOD'=\angle ABC=90^\circ$,
所以 $\triangle D'OE\backsim \triangle ABC$. -
若 $E$ 与原点 $O$ 重合,抛物线与射线 $OA$ 的另一个交点为点 $M$,过 $M$ 作 $MN\perp y$ 轴,垂足为 $N$.当 $m$ 为定值,抛物线与四边形 $ABCD$ 有公共点时,线段 $MN$ 的最大值为 $10$,请你探究 $a$ 的取值范围.标注答案$a$ 的取值范围是 $\dfrac 14\leqslant a\leqslant 1$解析当点 $E$ 与点 $O$ 重合时,点 $E$ 坐标为 $\left(0,0\right)$.
 因为抛物线 $y=ax^2+bx+n$ 过点 $E,A'$,
因为抛物线 $y=ax^2+bx+n$ 过点 $E,A'$,
所以 $\begin{cases}
n=0, \\ am^2+bm+n=-m,
\end{cases}$
化简得 $am+b=-1$,即 $b=-1-am$.
所以抛物线的解析式为 $y=ax^2-\left(1+am\right)x$.
因为抛物线与四边形 $ABCD$ 有公共点,
所以抛物线过点 $C$ 时的开口最大,过点 $A$ 时的开口最小.
当抛物线过点 $C\left(3m,0\right)$,此时 $MN$ 取最大值 $10$.
所以 $a\left(3m\right)^2-\left(1+am\right)\cdot 3m=0$,整理得 $am=\dfrac 12$.
抛物线的解析式为 $y=\dfrac {1}{2m}x^2-\dfrac 32x$.
由点 $A\left(2m,2m\right)$,可得直线 $OA$ 的解析式为 $y=x$.
联立方程组 $\begin{cases}
y=x, \\ y=\dfrac {1}{2m}x^2-\dfrac 32x.
\end{cases}$
化简得 $\dfrac 1{2m}x^2-\dfrac 52x=0$,
解得 $x_1=0, x_2=5m$,
所以 $MN=5m=10$,得 $m=2$.
此时 $a=\dfrac 14$.
当抛物线过点 $A\left(2m,2m\right)$,则 $a\left(2m\right)^2-\left(1+am\right)\cdot 2m=2m$.
解得 $am=2$.
又 $m=2$,此时 $a=1$.
故满足题意的 $a$ 的取值范围是 $\dfrac 14\leqslant a\leqslant 1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2