如图，已知直线 $y=-x+3$ 与 $x$ 轴、$y$ 轴分别交于 $A,B$ 两点，抛物线 $y=-x^2+bx+c$ 经过 $A,B$ 两点．点 $P$ 在线段 $OA$ 上，从点 $O$ 出发，向点 $A$ 以 $1 个单位{/}秒$ 的速度匀速运动；同时，点 $Q$ 在线段 $AB$ 上，从点 $A$ 出发，向点 $B$ 以 $\sqrt 2 个单位{/}秒$ 的速度匀速运动，连接 $PQ$，设运动时间为 $t$ 秒．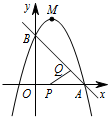
【难度】
【出处】
无
【标注】
-
问：当 $t$ 为何值时，$\triangle APQ$ 为直角三角形；标注答案当 $t=1$ 或 $t=\dfrac 32$ 时，$\triangle PQA$ 是直角三角形解析因为 $ OA=OB=3$，$\angle BOA=90^\circ$，
所以 $ \angle QAP=45^\circ$．
① 当 $\angle PQA=90^\circ$ 时，如图．
设运动时间为 $t$ 秒，则 $QA=\sqrt 2t$，$PA=3-t$．
在 $\mathrm {Rt}\triangle PQA$ 中，$\dfrac {QA}{PA}=\dfrac {\sqrt 2}{2}$，
即 $\dfrac {\sqrt 2t}{3-t}=\dfrac {\sqrt 2}{2}$，
解得 $t=1$．
② 当 $\angle QPA=90^\circ $ 时，如图．
设运动时间为 $t$ 秒，则 $QA=\sqrt 2t$，$PA=3-t$．
在 $\mathrm {Rt}\triangle PQA$ 中，$\dfrac {PA}{QA}=\dfrac {\sqrt 2}{2}$，
即 $\dfrac {3-t}{\sqrt 2t}=\dfrac {\sqrt 2}{2}$，
解得 $t=\dfrac 32$．
综上所述，当 $t=1$ 或 $t=\dfrac 32$ 时，$\triangle PQA$ 是直角三角形． -
设抛物线顶点为 $M$，连接 $BP,BM,MQ$，问：是否存在 $t$ 的值，使以 $B,Q,M$ 为顶点的三角形与以 $O,B,P$ 为顶点的三角形相似？若存在，请求出 $t$ 的值；若不存在，请说明理由．标注答案当 $t=\dfrac 94$ 时，以 $B,Q,M$ 为顶点的三角形与以 $O,B,P$ 为顶点的三角形相似解析因为 $ y=-x+3$ 与 $x$ 轴交于点 $A$，与 $y$ 轴交于点 $B$，
所以点 $A$ 的坐标为 $\left(3,0\right)$，点 $B$ 的坐标为 $\left(0,3\right)$，
将 $A\left(3,0\right),B\left(0,3\right)$ 代入 $y=-x^2+bx+c$，
得 $\begin{cases} -9+3b+c=0, \\ c=3.\end{cases}$
解得 $\begin{cases} b=2, \\ c=3.\end{cases}$
所以抛物线的解析式为 $y=-x^2+2x+3=-\left(x-1\right)^2+4$，
所以点 $M$ 的坐标为 $\left(1,4\right)$．
所以 $MB=\sqrt {1^2+1^2}=\sqrt 2$．
所以 $BM^2+AB^2=AM^2$．
所以 $\angle MBA=90^\circ$．
如图，设运动时间为 $t$ 秒，则 $OP=t$，$BQ=\left(3-t\right)\sqrt 2$．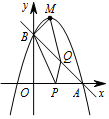
① 当 $\triangle BOP\backsim \triangle QBM$ 时，$\dfrac {MB}{OP}=\dfrac {BQ}{OB}$，
即 $\dfrac {\sqrt 2}{t}=\dfrac {\left(3-t\right)\sqrt 2}{3}$，
整理得 $t^2-3t+3=0$，
而 $\Delta=3^2-4\times 1\times 3<0$，所以此种情况不存在；
② 当 $\triangle BOP\backsim \triangle MBQ$ 时，$\dfrac {BM}{OB}=\dfrac {BQ}{OP}$，
即 $\dfrac {\sqrt 2}{3}=\dfrac {\left(3-t\right)\sqrt 2}{t}$，
解得 $t=\dfrac 94$．
所以当 $t=\dfrac 94$ 时，以 $B,Q,M$ 为顶点的三角形与以 $O,B,P$ 为顶点的三角形相似．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
