已知抛物线 $E_{1}:y=x^2$ 经过点 $A\left(1,m\right)$,以原点为顶点的抛物线 $E_{2}$ 经过点 $B\left(2,2\right)$,点 $A,B$ 关于 $y$ 轴的对称点分别为点 $A',B'$.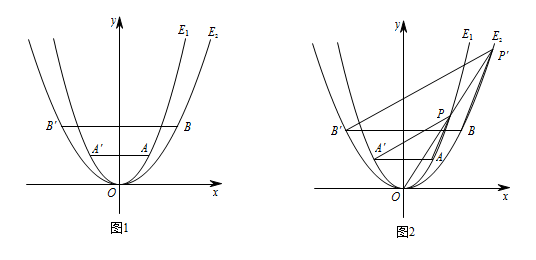

【难度】
【出处】
无
【标注】
-
如图1,在第一象限内,抛物线 $ E_{1} $ 上是否存在点 $ Q $,使得以点 $ Q ,B ,B' $ 为顶点的三角形为直角三角形?若存在,求出点 $ Q $ 的坐标;若不存在,请说明理由;标注答案存在,点 $Q$ 坐标为 $\left(2,4\right)$ 与 $\left(\sqrt 3 ,3\right)$解析可设它对应的函数表达式为 $y=ax^2\left(a\neq 0\right)$,
将点 $B\left(2,2\right)$ 坐标代入抛物线 $E_2$ 解析式,可得 $a=\dfrac 12$.
所以抛物线 $E_2$ 所对应的二次函数表达式为 $y=\dfrac12 x^2$.
如图,假设在第一象限内,抛物线 $E_1$ 上存在点 $Q$,使得 $\triangle QBB'$ 为直角三角形.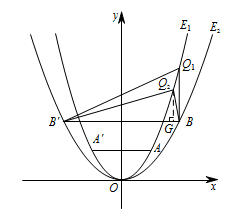 由图象可知直角顶点只能为点 $B$ 或点 $Q$.
由图象可知直角顶点只能为点 $B$ 或点 $Q$.
① 当点 $B$ 为直角顶点时,过 $B$ 作 $QB\perp BB'$ 交抛物线 $E_1$ 于 $Q$,
则点 $Q$ 与 $B$ 的横坐标相等且为 $2$,
将 $x=2$ 代入 $y=x^2$,得 $y=4$,
所以点 $Q$ 的坐标为 $\left(2,4\right)$.
② 当点 $Q$ 为直角顶点时,则有 $QB'^2+QB^2=B'B^2$,
过点 $Q$ 作 $GQ\perp BB'$ 于点 $G$,
设点 $Q$ 的坐标为 $\left(t,t^2\right)\left(t>0\right)$,
则有 $\left(t+2\right)^2+\left(t^2-2\right)^2+\left(2-t\right)^2+\left(t^2-2\right)^2=4^2$,
整理得 $t^4-3t^2=0$,
解得 $t_1= \sqrt 3$,$t_2=-\sqrt 3$(舍去),$t_3=0$(舍去),
所以点 $Q$ 的坐标为 $\left(\sqrt 3 ,3\right)$,
综上可得,存在符合条件的点 $Q$,其坐标为 $\left(2,4\right)$ 与 $\left(\sqrt 3 ,3\right)$. -
如图2,$ P $ 为第一象限内的抛物线 $ E_{1} $ 上与点 $ A $ 不重合的一点,连接 $ OP $ 并延长与抛物线 $ E_{2} $ 相交于点 $ P' $,求 $ \triangle PAA'$ 与 $\triangle P'BB' $ 的面积之比.标注答案$\dfrac{S_{\triangle PAA'}}{S_{\triangle P'BB'}}=\dfrac 14$解析由题意可得 $m=1$,所以点 $(1,1)$.
如图,过点 $P$ 作 $PC\perp x$ 轴,垂足为点 $C$,$PC$ 交直线 $AA'$ 于点 $E$;过点 $P'$ 作 $P'D\perp x$ 轴,垂足为点 $D$,$P'D$ 交直线 $BB'$ 于点 $F$.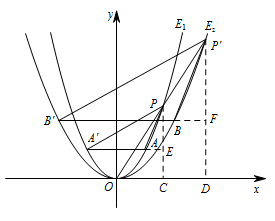 依题意可设 $ P\left(c,c^2\right),P'\left(d,\dfrac12d^2\right)$,其中 $c>0, c\neq 1$,
依题意可设 $ P\left(c,c^2\right),P'\left(d,\dfrac12d^2\right)$,其中 $c>0, c\neq 1$,
由 $\tan \angle POC=\tan \angle P'OD $,可得 $\dfrac{c^2}{c}=\dfrac{\dfrac 12d^2}{d} $,
所以 $d=2c$.
所以 $\dfrac{S_{\triangle PAA'}}{S_{\triangle P'BB'}}=\dfrac{\dfrac 12 AA'\cdot PE}{\dfrac 12 BB'\cdot P'F}=\dfrac{\dfrac 12\times 2\times {\left|{c^2-1}\right|}}{\dfrac 12\times 4\times {\left|{\dfrac 12d^2-2}\right|}}=\dfrac{{\left|{c^2-1}\right|}}{2\times {\left|{2c^2-2}\right|}}=\dfrac 14$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2