若关于 $x$ 的二次函 $y=a{x^2} + bx + c$($a>0,c>0$,$a,b,c$ 是常数)与 $x$ 轴交于两个不同的点 $A\left(x_1,0\right),B\left(x_2,0\right)$($0<x_1<x_2$),与 $y$ 轴交于点 $P$,其图象顶点为点 $M$,点 $O$ 为坐标原点.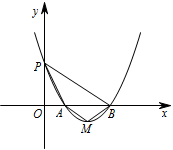

【难度】
【出处】
无
【标注】
-
当 $x_1=2c$ 时,试问 $\triangle ABM$ 能否为等边三角形?判断并证明你的结论;标注答案$\triangle ABM$ 不可能为等边三角形解析当 $x_1=2c$ 时,$x_2=\dfrac{\dfrac ca}{x_1}=\dfrac1{2a}$,
此时 $b=-a\left(x_1+x_2\right)=-\left(2ac+\dfrac12\right)$,$4ac=-2b-1$.
因为点 $M$ 的坐标为 $\left(-\dfrac{b}{2a},\dfrac{4ac-b^2}{4a}\right)$,
若 $\triangle ABM$ 为等边三角形,则有 $\left|\dfrac{4ac-b^2}{4a} \right|=\dfrac{\sqrt3}{2}AB$,
即 $\dfrac{b^2-4ac}{4a}=\dfrac{\sqrt3}{2}\left(\dfrac{1}{2a}-2c\right)$,
所以 $\dfrac{b^2+2b+1}{4a}=\dfrac{\sqrt3}{2}\cdot \dfrac{1+2b+1}{2a}$,
所以 $b^2+2b+1=\sqrt3\cdot\left(1+2b+1\right)$,
解得 $b_1=-1, b_2=2\sqrt3-1>0(舍去)$.
此时 $4ac=1$,即 $2c=\dfrac1{2a}$,
那么点 $A,B$ 重合,
故 $\triangle ABM$ 不可能为等边三角形. -
当 $x_1=mc$($m<0$)时,记 $\triangle MAB,\triangle PAB$ 的面积分别为 $S_1,S_2$,若 $\triangle BPO\backsim \triangle PAO$,且 $S_1=S_2$,求 $m$ 的值.标注答案$m=\sqrt2-1$解析因为 $\triangle BPO\backsim \triangle PAO$,
所以 $\dfrac{OP}{AO}=\dfrac{BO}{OP}$,
即 $x_1x_2=c^2=\dfrac ca$,
因为 $x_1x_2=\dfrac ca$,
所以 $ac=1$.
因为 $S_1=S_2$,
所以 $c= \left|\dfrac{4ac-b^2}{4a} \right|=\dfrac{b^2}{4a}-c$,
所以 $b^2=4a\cdot 2c=8ac=8$,
所以 $b_1=-2\sqrt2, b_2=2\sqrt2>0(舍)$.
方程可化为 $\dfrac1cx^2-2\sqrt2x+c=0$,
解得 $x_1=\left(\sqrt2-1\right)c, x_2=\left(\sqrt2+1\right)c$.
所以 $m_1=\sqrt2-1, m_2=\sqrt2+1>0(舍)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2