在平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-2mx+m^2-m+2$，线段 $AB$ 的两个端点分别为 $A(-3,m),B(1,m)$．若线段 $AB$ 与该抛物线只有一个公共点，结合函数图象，求 $m$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$m$ 的取值范围为 $1\leqslant m\leqslant 3$
【解析】
由题意可得当 $-3\leqslant x\leqslant 1$ 时，$x^2-2mx+m^2-m+2=m$ 有且只有一个解．
整理方程得 $(x-m)^2=2(m-1)$，
所以 $m-1\geqslant 0$，即 $ m \geqslant 1$．
此时方程的解为 $x_1=m-\sqrt{2(m-1)}, x_2=m+\sqrt{2(m-1)}$．
如图所示，可得 $\begin{cases}m-\sqrt{2(m-1)}\geqslant -3,& ① \\ m-\sqrt{2(m-1)}\leqslant 1.& ② \end{cases}$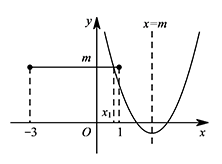
由 ① 得 $(m+2)^2+7\leqslant 0$，此不等式恒成立；
由 ② 得 $1\leqslant m\leqslant 3$．
综上可得，满足题意的 $m$ 的取值范围为 $1\leqslant m\leqslant 3$．
整理方程得 $(x-m)^2=2(m-1)$，
所以 $m-1\geqslant 0$，即 $ m \geqslant 1$．
此时方程的解为 $x_1=m-\sqrt{2(m-1)}, x_2=m+\sqrt{2(m-1)}$．
如图所示，可得 $\begin{cases}m-\sqrt{2(m-1)}\geqslant -3,& ① \\ m-\sqrt{2(m-1)}\leqslant 1.& ② \end{cases}$
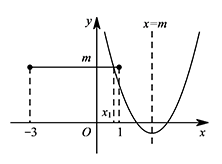由 ① 得 $(m+2)^2+7\leqslant 0$，此不等式恒成立；由 ② 得 $1\leqslant m\leqslant 3$．
综上可得，满足题意的 $m$ 的取值范围为 $1\leqslant m\leqslant 3$．
答案
解析
备注
