已知二次函数 $y=ax^2+2ax+a-1 (a>0)$．结合函数图象回答：当 $x\geqslant 1$ 时，其对应的函数值 $y$ 的最小值的范围是 $2\leqslant y\leqslant 6$，求 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$a$ 的取值范围为 $\dfrac 34\leqslant a\leqslant \dfrac 74$
【解析】
由 $y=ax^2+2ax+a-1=a(x+1)^2-1$，得抛物线的顶点坐标为 $(-1,-1)$．
而 $a>0$，所以当 $x\geqslant 1$ 时，$y$ 随着 $x$ 的增大而增大．
把 $(1,2)$ 代入二次函数解析式，得 $a=\dfrac 34$；
把 $(1,6)$ 代入二次函数解析式，得 $a=\dfrac 74$．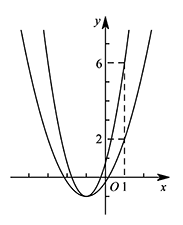
结合图象，满足题意的 $a$ 的取值范围为 $\dfrac 34\leqslant a\leqslant \dfrac 74$．
而 $a>0$，所以当 $x\geqslant 1$ 时，$y$ 随着 $x$ 的增大而增大．
把 $(1,2)$ 代入二次函数解析式，得 $a=\dfrac 34$；
把 $(1,6)$ 代入二次函数解析式，得 $a=\dfrac 74$．
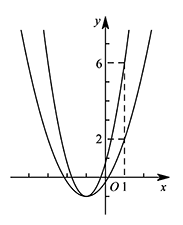结合图象，满足题意的 $a$ 的取值范围为 $\dfrac 34\leqslant a\leqslant \dfrac 74$．
答案
解析
备注
