在正方形 $ABCD$ 中，点 $E$ 是对角线 $AC$ 上的动点（与点 $A,C$ 不重合），连接 $BE$．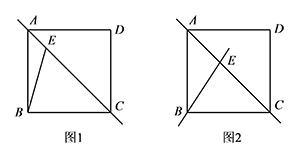
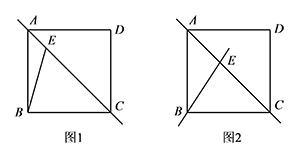
【难度】
【出处】
无
【标注】
-
将射线 $BE$ 绕点 $B$ 顺时针旋转 $45^\circ$，交直线 $AC$ 于点 $F$．补全图1，并探究 $AE,CF,EF$ 之间的数量关系．标注答案$AE^2+FC^2=EF^2$解析
解法一 如图，将 $\triangle BAE$ 绕点 $B$ 顺时针旋转 $90^\circ$ 至 $\triangle BCG$，连接 $FG$．
由旋转可得 $\angle EBF=45^\circ$，$BE=BG$，$CG=AE$，$\angle EBG=90^\circ$，$\angle BCG=\angle BAE=45^\circ$，
从而证得 $\triangle BEF\cong \triangle BGF (\rm{SAS})$，
所以 $GF=EF$．
而 $\angle FCG=\angle FCB+\angle BCG=90^\circ$，
所以 $CF^2+CG^2=GF^2$，
即 $AE^2+FC^2=EF^2$．解法二 如图，将 $\triangle ABE$ 沿着 $BE$ 翻折得到 $\triangle HBE$，连接 $FH$．
由翻折可得 $\angle HBE=\angle ABE$，$\angle BHE=\angle BAE=45^\circ$，$HE=AE$，$HB=AB=CB$．
而 $\angle EBF=45^\circ$，
所以 $\angle ABE+\angle CBF=\angle HBE+\angle HBF$，
从而 $\angle CBF=\angle HBF$，
所以 $\triangle CBF\cong \triangle HBF (\rm{SAS})$．
所以 $\angle BHF=\angle BCF=45^\circ$，$FH=FC$．
所以 $\angle EHF=90^\circ$，
故而 $HE^2+HF^2=EF^2$，
即 $AE^2+CF^2=EF^2$． -
如图2，若将直线 $BE$ 绕点 $B$ 顺时针旋转 $135^\circ$，交直线 $AC$ 于点 $F$．直线 $AC$ 上存在三条线段满足：其中两条线段的平方和等于第三条线段的平方，请直接用等式表示这三条线段的数量关系．标注答案$AF^2+CE^2=EF^2$解析如图，将 $\triangle BAF$ 绕点 $B$ 顺时针旋转 $90^\circ$ 至 $\triangle BCG$，连接 $EG$．
同上可证 $\triangle BEF\cong \triangle BEG$，再证 $\angle ECG=90^\circ$，
从而得到 $CG^2+CE^2=EG^2$，即 $AF^2+CE^2=EF^2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
