在平面直角坐标系 $xOy$ 中，对“隔离直线”给出如下定义：
点 $P(x,m)$ 是图形 $G_1$ 上的任意一点，点 $Q(x,n)$ 是图形 $G_2$ 上的任意一点，若存在直线 $l:y=kx+b(k\ne 0)$ 满足 $m\leqslant kx+b$ 且 $n\geqslant kx+b$，则称直线 $l:y=kx+b(k\ne 0)$ 的图形 $G_1$ 与 $G_2$ 的“隔离直线”．
如图1，直线 $l:y=-x-4$ 是函数 $y=\dfrac 6x(x<0)$ 的图象与正方形 $OABC$ 的一条“隔离直线”．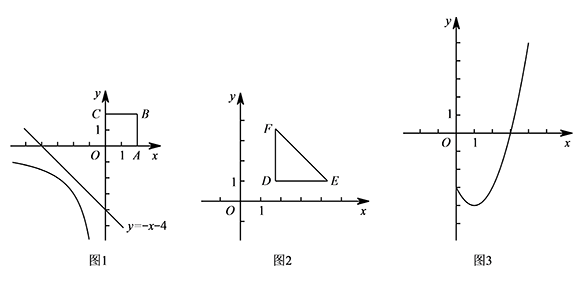
点 $P(x,m)$ 是图形 $G_1$ 上的任意一点，点 $Q(x,n)$ 是图形 $G_2$ 上的任意一点，若存在直线 $l:y=kx+b(k\ne 0)$ 满足 $m\leqslant kx+b$ 且 $n\geqslant kx+b$，则称直线 $l:y=kx+b(k\ne 0)$ 的图形 $G_1$ 与 $G_2$ 的“隔离直线”．
如图1，直线 $l:y=-x-4$ 是函数 $y=\dfrac 6x(x<0)$ 的图象与正方形 $OABC$ 的一条“隔离直线”．
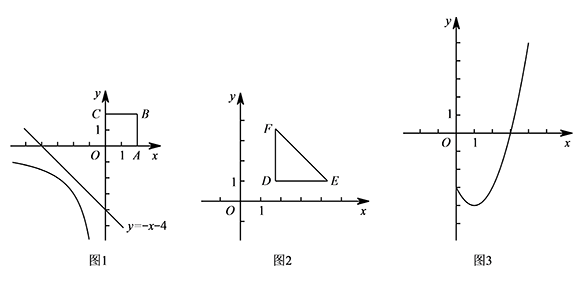
【难度】
【出处】
无
【标注】
-
在直线 $y_1=-2x$，$y_2=3x+1$，$y_3=-x+3$ 中，是图1函数 $y=\dfrac 6x(x<0)$ 的图象与正方形 $OABC$ 的“隔离直线”的为
-
如图2，第一象限的等腰直角 $\triangle EDF$ 的两腰分别与坐标轴平行，直角顶点 $D$ 的坐标是 $(\sqrt 3,1)$，$\odot O$ 的半径为 $2$．是否存在 $\triangle EDF$ 与 $\odot O$ 的"隔离直线"？若存在，求出“隔离直线”的表达式；若不存在，请说明理由．标注答案存在，“隔离直线”的表达式为 $y=-\sqrt 3x+4$解析如图，连接 $OD$，作直线 $DG\perp OD$ 交 $y$ 轴于点 $G$，作 $DH\perp x$ 轴于点 $H$．
由点 $D$ 的坐标可得 $OH=\sqrt 3,DH=1$
所以 $OD=\sqrt{OH^2+DH^2}=2$，$\tan \angle DOH=\dfrac{DH}{OH}=\dfrac{\sqrt 3}{3}$，
从而 $\angle DOH=30^\circ$，$\angle DOG=60^\circ$，
所以 $OG=2OD=4$，即点 $D(0,4)$．
由 $D,G$ 两点坐标可得直线 $DG$ 的表达式为 $y=-\sqrt 3x+4$．
即所求的“隔离直线”的表达式为 $y=-\sqrt 3x+4$． -
正方形 $A_1B_1C_1D_1$ 的一边在 $y$ 轴上，其它三边都在 $y$ 轴的右侧，点 $M(1,t)$ 是此正方形的中心．若存在直线 $y=2x+b$ 是函数 $y=x^2-2x-3 (0\leqslant x\leqslant 4)$ 的图象与正方形 $A_1B_1C_1D_1$ 的“隔离直线”，请直接写出 $t$ 的取值范围．标注答案$t\leqslant -8$ 或 $t\geqslant 2$解析根据题意可知正方形 $A_1B_1C_1D_1$ 的边长为 $2$，
从而由点 $M(1,t)$，得到点 $A_1(0,t-1),B_1(2,t-1),C_1(2,t+1),D_1(0,t+1)$．
① 令函数 $y=x^2-2x-3 (0\leqslant x\leqslant 4)$ 的图象的两端点为 $P(0,-3),Q(4,5)$．
得到 $PQ$ 的表达式为 $y=2x-3$．
如图，当点 $B_1$ 在直线 $PQ$ 上时，得 $t=2$．
② 直线 $y=2x+b$ 是函数 $y=x^2-2x-3 (0\leqslant x\leqslant 4)$ 的图象只有一个交点，
则方程组 $\begin{cases}y=2x+b,\\y=x^2-2x-3\end{cases}$ 只有一个解，
得到 $x^2-4x-3-b=0$ 只有一个解．
从而 $\Delta=16-4\times(-3-b)=28-4b=0$，即 $b=7$．
如图，当点 $D_1$ 在直线 $y=2x-7$ 上时，得 $t=-8$．
综上所述，结合图象，满足题意的 $t$ 的取值范围为 $t\leqslant -8$ 或 $t\geqslant 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
