在平面直角坐标系 $xOy$ 中，抛物线 $y=mx^2-2mx+2 (m\ne 0)$ 与 $y$ 轴交于点 $A$，其对称轴与 $x$ 轴交于点 $B$，点 $C,D$ 在 $x$ 轴上（点 $C$ 在点 $D$ 的左侧），且与点 $B$ 的距离都为 $2$，若抛物线与线段 $BC$ 有两个公共点，结合函数的图象，求 $m$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$m$ 的取值范围为 $m>2$ 或 $m\leqslant -\dfrac 23$
【解析】
因为抛物线 $y=mx^2-2mx+2=m(x-1)^2+2-m$，
所以抛物线的顶点为 $(1,2-m)$，对称轴为 $x=1$，点 $A(0,2)$．
所以点 $B$ 的坐标为 $(1,0)$，
从而点 $C(-1,0),D(3,0)$．
① 若 $m>0$，如图．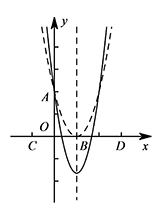
当顶点 $(1,2-m)$ 位于 $x$ 轴下方时，抛物线与 $CD$ 轴有两个交点．
所以 $2-m<0$，即 $m>2$．
② 若 $m<0$，如图．
若抛物线经过点 $C,D$，则 $m=-\dfrac 23$．
当 $m\leqslant -\dfrac 23$ 时，抛物线与 $CD$ 有两个交点．
综上所述，$m$ 的取值范围为 $m>2$ 或 $m\leqslant -\dfrac 23$．
所以抛物线的顶点为 $(1,2-m)$，对称轴为 $x=1$，点 $A(0,2)$．
所以点 $B$ 的坐标为 $(1,0)$，
从而点 $C(-1,0),D(3,0)$．
① 若 $m>0$，如图．
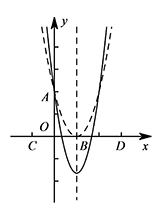当顶点 $(1,2-m)$ 位于 $x$ 轴下方时，抛物线与 $CD$ 轴有两个交点．所以 $2-m<0$，即 $m>2$．
② 若 $m<0$，如图．
若抛物线经过点 $C,D$，则 $m=-\dfrac 23$．当 $m\leqslant -\dfrac 23$ 时，抛物线与 $CD$ 有两个交点．
综上所述，$m$ 的取值范围为 $m>2$ 或 $m\leqslant -\dfrac 23$．
答案
解析
备注
