$ 1 $

记函数 $g(x)=\dfrac 1x + \ln x$，则$$g'(x)=\dfrac{x-1}{x^2},$$于是可得函数 $g(x)$ 的图象如图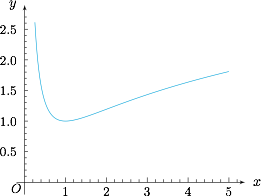．于是当 $a=2$ 时，$f(x)$ 在 $\left(1,{\mathrm e}^2\right)$ 上有一个零点；

$\{1\}$

若 $f(x)$ 恰有一个零点，$a$ 的取值集合为 $\{1\}$．

略

问题的关键是第三问的不等式的证明．
先证明左边的不等式．
{\color{cyan}\bf{齐次化}}
根据题意，有$$\dfrac{1}{x_1}+\ln x_1=a,\quad\dfrac{1}{x_2}+\ln x_2=a,$$两式相减，化简得$$x_1x_2=\dfrac{x_2-x_1}{\ln{\dfrac{x_2}{x_1}}},$$于是可得$$x_1=\dfrac{1-\dfrac{x_1}{x_2}}{\ln{\dfrac{x_2}{x_1}}},\quad x_2=\dfrac{\dfrac{x_2}{x_1}-1}{\ln\dfrac{x_2}{x_1}},$$令 $\dfrac{x_2}{x_1}=t$，其中 $t>1$，则$$x_1+x_2=\dfrac{1-\dfrac 1t}{\ln t}+\dfrac{t-1}{\ln t}=\dfrac{t-\dfrac 1t}{\ln t},$$因此只需要证明$$\forall t>1,t-\dfrac 1t-2\ln t>0.$$考虑到$$\left(t-\dfrac 1t-2\ln t\right)'_t=\left(\dfrac 1t-1\right)^2>0,$$于是左边不等式得证．
{\color{cyan}\bf{对称构造}}
令 $g(x)=\dfrac{1}{x}+\ln x$，证明$$\forall t\in (0,1),g(1-t)>g(1+t)$$即可．事实上，有$$g(1-t)-g(1+t)=\dfrac{2t}{1-t^2}+\ln\dfrac{1-t}{1+t},$$考虑到$$\left(\dfrac{2t}{1-t^2}+\ln\dfrac{1-t}{1+t}\right)'_t=\dfrac{4t^2}{\left(1-t^2\right)^2}>0,$$于是左边不等式得证．
再证明右边的不等式．
{\color{cyan}\bf{齐次化}}
右边的不等式等价于$$\ln\dfrac{x_1+x_2+1}{3}+1-a<0,$$将$$x_1+x_2=\dfrac{t^2-1}{t\ln t},\quad a=\dfrac {1}{x_1}+\ln x_1=\dfrac{t\ln t}{t-1}+\ln\dfrac{t-1}{t\ln t},$$代入，该不等式左边为$$\ln\dfrac{t^2-1+t\ln t}{t-1}-\dfrac{t\ln t}{t-1}+1-\ln 3,$$其导函数为$$\dfrac{t\ln^2t-(t-1)^2}{\left(t^2-1+t\ln t\right)\left(t-1\right)^2}.$$因此只需要证明$$\forall t>1,\sqrt t\ln t-t+1<0,$$即$$\forall t>1,2\ln \sqrt t<\sqrt t-\dfrac{1}{\sqrt t},$$根据第（1）小问，于是右边不等式得证．
{\color{cyan}\bf{放缩法}}
令 $x_0={\mathrm e}^{a-1}$，则 $1+\ln x_0-a=0$，于是可知 $x_0$ 是函数$$h(x)=1+x\ln x -ax$$的极小值点．根据题意，有$$x_1<x_0<x_2,$$于是$$\dfrac{x_1}{x_0}<1<\dfrac{x_2}{x_0},$$应用我们熟知的不等式$$\forall x\in (0,1),\ln x<\dfrac{2(x-1)}{x+1},\quad \forall x>1,\ln x>\dfrac{2(x-1)}{x+1},$$可得$$\ln\dfrac{x_1}{x_0}<\dfrac{2(x_1-x_0)}{x_1+x_0},\quad \ln\dfrac{x_2}{x_0}>\dfrac{2(x_2-x_0)}{x_2+x_0}.$$又$$\ln x_1=a-\dfrac{1}{x_1}=1+\ln x_0-\dfrac{1}{x_1},$$从而有$$\ln\dfrac{x_1}{x_0}=1-\dfrac 1{x_1},$$同理有$$\ln\dfrac{x_2}{x_0}=1-\dfrac 1{x_2},$$这样就有$$1-\dfrac{1}{x_1}<\dfrac{2(x_1-x_0)}{x_1+x_0},\quad 1-\dfrac{1}{x_2}>\dfrac{2(x_2-x_0)}{x_2+x_0},$$从而可得$$(3x_1-1)x_0-x_1^2-x_1<0<(3x_2-1)x_0-x_2^2-x_2,$$即$$3(x_2-x_1)x_0-(x_2-x_1)(x_2+x_1+1)>0,$$两边同除以 $x_2-x_1$，即得$$x_1+x_2<3x_0-1=3{\mathrm e}^{a-1}-1,$$于是右边不等式得证．