如图，矩形 $ABCD$ 中，$AB=6 \mathrm{cm}$，$BC=\sqrt 5 \mathrm{cm}$，对角线 $AC,BD$ 相交于点 $O$，$\triangle COD$ 关于 $CD$ 的对称图形为 $\triangle CED$．连接 $AE$，若点 $P$ 为线段 $AE$ 上一动点（不与点 $A$ 重合），连接 $OP$．一动点 $Q$ 从点 $O$ 出发，以 $1 \mathrm{cm{/}s}$ 的速度沿线段 $OP$ 匀速运动到点 $P$，再以 $1.5 \mathrm{cm{/}s}$ 的速度沿线段 $PA$ 匀速运动到点 $A$，到达点 $A$ 后停止运动．当点 $Q$ 沿上述路线运动到点 $A$ 所需要的时间最短时，求 $AP$ 的长和点 $Q$ 走完全程所需的时间．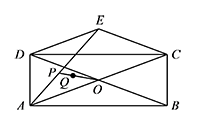
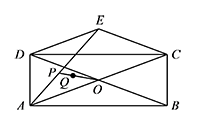
【难度】
【出处】
无
【标注】
【答案】
$AP$ 的长为 $\dfrac 32 \mathrm{cm}$，点 $Q$ 走完全程所需的时间为 $3 \mathrm{s}$
【解析】
由题意可得点 $Q$ 运动到点 $A$ 的时间为 $t=\left(\dfrac{PO}{1}+\dfrac{PA}{1.5}\right)\mathrm{s}=\left(PO+\dfrac 23PA\right)\mathrm{s}$．
过点 $E$ 作 $EF\perp AD$ 交 $AD$ 的 延长线于点 $F$．
则 $EF=3 \mathrm{cm}$，$AF=\dfrac 32\sqrt 5 \mathrm{cm}$，
所以 $AE=\sqrt{EF^2+AF^2}=\dfrac 92 \mathrm{cm}$，
从而 $\sin\angle EAF=\dfrac{EF}{EA}=\dfrac23$．
过点 $P$ 作 $PG\perp AD$ 于点 $G$，则有 $PG=\dfrac 23PA$．
过点 $O$ 作 $OH\perp AD$ 于点 $H$，则 $OH=\dfrac 12CD=3$．
而 $PO+\dfrac 23PA=PO+PG\geqslant OH$，所以 $t_{\text{最小}}=3 \mathrm{s}$．
显然 $AH=\dfrac 13 AF$，所以 $AP=\dfrac 13 AE=\dfrac 32 \mathrm{cm}$．
综上所述，当点 $Q$ 沿上述路线运动到点 $A$ 所需要的时间最短时，$AP$ 的长为 $\dfrac 32 \mathrm{cm}$，点 $Q$ 走完全程所需的时间为 $3 \mathrm{s}$．
过点 $E$ 作 $EF\perp AD$ 交 $AD$ 的 延长线于点 $F$．
则 $EF=3 \mathrm{cm}$，$AF=\dfrac 32\sqrt 5 \mathrm{cm}$，所以 $AE=\sqrt{EF^2+AF^2}=\dfrac 92 \mathrm{cm}$，
从而 $\sin\angle EAF=\dfrac{EF}{EA}=\dfrac23$．
过点 $P$ 作 $PG\perp AD$ 于点 $G$，则有 $PG=\dfrac 23PA$．
过点 $O$ 作 $OH\perp AD$ 于点 $H$，则 $OH=\dfrac 12CD=3$．
而 $PO+\dfrac 23PA=PO+PG\geqslant OH$，所以 $t_{\text{最小}}=3 \mathrm{s}$．
显然 $AH=\dfrac 13 AF$，所以 $AP=\dfrac 13 AE=\dfrac 32 \mathrm{cm}$．
综上所述，当点 $Q$ 沿上述路线运动到点 $A$ 所需要的时间最短时，$AP$ 的长为 $\dfrac 32 \mathrm{cm}$，点 $Q$ 走完全程所需的时间为 $3 \mathrm{s}$．
答案
解析
备注
