在平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-2mx+m^2+m$ 的顶点为 $C$．直线 $y=x+2$ 与抛物线交于 $A,B$ 两点，点 $A$ 在抛物线的对称轴左侧，抛物线的对称轴与直线 $AB$ 交于点 $M$，作点 $B$ 关于直线 $MC$ 的对称点 $B'$．以 $M$ 为圆心、$MC$ 为半径的圆上存在一点 $Q$，使得 $QB'+\dfrac{\sqrt 2}{2}QB$ 的值最小，则最小值为多少？
【难度】
【出处】
无
【标注】
【答案】
$QB'+\dfrac{\sqrt 2}{2}QB$ 的最小值为 $\sqrt {10}$
【解析】
因为 $y=x^2-2mx+m^2+m=\left(x-m\right)^2+m$，
所以顶点 $C$ 的坐标为 $\left(m,m\right)$，
从而点 $M$ 的坐标为 $\left(m,m+2\right)$．
所以 $QM=CM=2$．
联立方程组 $\begin{cases}y=x^2-2mx+m^2+m,\\y=x+2.\end{cases}$
可得点 $A,B$ 的坐标分别为 $\left(m-1,m+1\right), \left(m+2,m+4\right)$．
所以 $BM=2\sqrt 2$，即 $QM=\dfrac{\sqrt 2}2BM$．
取 $BM$ 的中点 $N$，则 $NM=\dfrac{\sqrt 2}2QM$，
连接 $QN$，则 $\triangle QMB\backsim\triangle NMQ$，
从而 $QN=\dfrac {\sqrt 2}{2}QB$．
连接 $B'N$，则 $B'N$ 即为 $QB'+\dfrac{\sqrt 2}{2}QB$ 的最小值．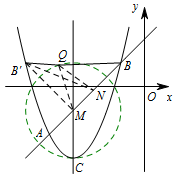
易得 $\angle AMC=45^\circ$，
连接 $B'M$，则 $\angle B'MB=90^\circ$．
在 $\mathrm {Rt}\triangle B'MN$ 中，$B'N=\sqrt {10}$．
即 $QB'+\dfrac{\sqrt 2}{2}QB$ 的最小值为 $\sqrt {10}$．
所以顶点 $C$ 的坐标为 $\left(m,m\right)$，
从而点 $M$ 的坐标为 $\left(m,m+2\right)$．
所以 $QM=CM=2$．
联立方程组 $\begin{cases}y=x^2-2mx+m^2+m,\\y=x+2.\end{cases}$
可得点 $A,B$ 的坐标分别为 $\left(m-1,m+1\right), \left(m+2,m+4\right)$．
所以 $BM=2\sqrt 2$，即 $QM=\dfrac{\sqrt 2}2BM$．
取 $BM$ 的中点 $N$，则 $NM=\dfrac{\sqrt 2}2QM$，
连接 $QN$，则 $\triangle QMB\backsim\triangle NMQ$，
从而 $QN=\dfrac {\sqrt 2}{2}QB$．
连接 $B'N$，则 $B'N$ 即为 $QB'+\dfrac{\sqrt 2}{2}QB$ 的最小值．
易得 $\angle AMC=45^\circ$，连接 $B'M$，则 $\angle B'MB=90^\circ$．
在 $\mathrm {Rt}\triangle B'MN$ 中，$B'N=\sqrt {10}$．
即 $QB'+\dfrac{\sqrt 2}{2}QB$ 的最小值为 $\sqrt {10}$．
答案
解析
备注
