已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的两个焦点与短轴的一个端点是直角三角形的三个顶点．直线 $l:y=-x+3$ 与椭圆 $E$ 有且只有一个公共点 $T$．
【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的方程及点 $T$ 的坐标；标注答案$\dfrac{x^2}6+\dfrac{y^2}3=1$，$T(2,1)$解析根据勾股定理，可得 $a^2+a^2=(2c)^2$，其中 $c$ 为椭圆的半焦距．又由直线 $l$ 与椭圆联立的等效判别式\footnote{直线 $Ax+By+C=0$ 与椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 联立后的判别式与等效判别式 $\Delta_0=a^2A^2+b^2B^2-C^2$ 同号，这很容易利用联立方程证明．}可得$$a^2\cdot 1^2+b^2\cdot 1^2-(-3)^2=0,$$于是可得方程组$$a^2=2c^2,a^2+b^2=9,a^2=b^2+c^2,a^2=6, b^2=3,c^2=3,$$于是椭圆 $E$ 的方程为 $\dfrac{x^2}6+\dfrac{y^2}3=1$，进而不难求出 $T(2,1)$．
-
设 $O$ 是坐标原点，直线 $l'$ 平行于 $OT$，与椭圆 $E$ 交于不同的两点 $A,B$，且与直线 $l$ 交于点 $P$．证明：存在常数 $\lambda$，使得 $|PT|^2=\lambda |PA|\cdot |PB|$，并求 $\lambda$ 的值．标注答案$\lambda= \dfrac{4}{5} $解析
解法1 注意到问题的结论类似于圆幂定理，因此考虑用仿射变换．作仿射变换 $x'=x$，$y'=\sqrt 2y$ 则椭圆 $E$ 变为圆$$E':x'^2+y'^2=6,$$此时设 $P,A,B,T$ 的对应点分别是 $P',A',B',T'$．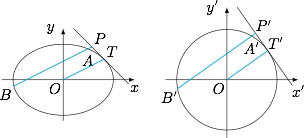
由仿射变换前后的弦长对应关系，可得$$\dfrac{|P'T'|^2}{|PT|^2}=\dfrac{1+2\cdot (-1)^2}{1+(-1)^2}=\dfrac 32,$$而$$\dfrac{|P'A'|\cdot |P'B'|}{|PA|\cdot |PB|}=\dfrac{1+2\cdot\left(\dfrac 12\right)^2}{1+\left(\dfrac 12\right)^2}=\dfrac 65,$$两式相比，可得$$\dfrac{|PT|^2}{|PA|\cdot |PB|}\cdot \dfrac{|P'A'|\cdot |P'B'|}{|P'T'|^2}=\dfrac 45,$$而根据圆幂定理，有$$|P'T'|^2=|P'A'|\cdot |P'B'|,$$因此原命题得证，且 $\lambda=\dfrac 45$．解法2 设 $P$ 点坐标为 $(p,3-p)$，由题意，可设直线 $l'$ 的参数方程为$$\begin{cases}x=p+2t,\\y=3-p+t,\end{cases}$$其中 $t$ 为参数．将其与椭圆方程联立，得$$2t^2+4t+p^2-4p+4=0.$$设 $A,B$ 两点对应的参数分别为 $t_1,t_2$，则$$\begin{cases}\Delta>0,\\t_1+t_2=-2,\\t_1t_2= \dfrac{(p-2)^2}{2}. \end{cases}$$因为$$|PT|^2=2(p-2)^2, |PA|\cdot|PB|=\sqrt{5}|t_1|\cdot\sqrt{5}|t_2|=\dfrac{5(p-2)^2}{2},$$所以存在常数 $\lambda= \dfrac{4}{5} $，使得 $|PT|^2=\lambda |PA|\cdot |PB|$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
