数列 $\{x_{n}\}$ 满足 $x_{1}=0$,$x_{n+1}=-x_{n}^{2}+x_{n}+c(n\in\mathbb{N}^{*})$.
【难度】
【出处】
2012年高考安徽卷(理)
【标注】
-
证明:$\{x_{n}\}$ 是递减数列的充分必要条件是 $c<0$;标注答案略解析
充分性的证明 $c<0$ 时,$$\Delta x_{n}=x_{n+1}-x_{n}=-x_{n}^{2}+c<0,$$所以数列 $\{x_{n}\}$ 是递减数列;必要性的证明 $x_{1}=0$,$x_{2}=c$,$\{x_{n}\}$ 递减时,一定有 $c<0$.
综上所述,原命题得证. -
求 $c$ 的取值范围,使 $\{x_{n}\}$ 是递增数列.标注答案$\left(0,\dfrac 14\right]$解析不难证明 $0<c<1$.
考虑到函数 $f(x)=-x^{2}+x+c$ 的对称轴为 $x=\dfrac 12$,不动点为 $\pm\sqrt{c}$,因此有两种情形: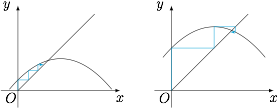
情形一 $\sqrt{c}\leqslant \dfrac{1}{2}$.此时函数图象如左图,容易证明 $x_{n}\in\big[-\sqrt{c},\sqrt{c} \big]$,于是 $f(x_{n})>x_{n}$,即 $x_{n+1}>x_{n}$,即数列 $\{x_{n}\}$ 单调递增.情形二 $\sqrt{c}>\dfrac{1}{2}$.此时函数图象如右图,此时 $\{x_{n}\}$ 应为摆动数列,考虑用反证法.
只需要证明数列中存在某项 $x_{k}>\dfrac 12$ 即可.这是因为,若 $x_k\in\left(\dfrac{1}{2},\sqrt{c}\right)$,则 $x_{k+1}>\sqrt c$,$x_{k+2}<\sqrt{c}$;若 $x_k>\sqrt c$,则 $x_{k+1}<\sqrt c$,均与数列 $\{x_n\}$ 单调递增矛盾.
也就是说只需要证明若 $\{x_{n}\}$ 单调递增,则 $\{x_{n}\}$ 的极限为 $\sqrt c$,就可以推出矛盾.
事实上,$$\sqrt c-x_{n+1}<\left(\sqrt c-x_{n}\right)\left(1-\sqrt c-x_{n}\right)<\left(1-\sqrt c\right)\left(\sqrt c-x_{n}\right),$$于是$$\sqrt c-x_{n+1}<\left(1-\sqrt c\right)^{n}\left(\sqrt c-x_{1}\right)=\sqrt c\left(1-\sqrt c\right)^{n},$$因此 $\{x_{n}\}$ 的极限为 $\sqrt c$,从而必然存在某项 $x_k>\dfrac 12$.
综上所述,$c$ 的取值范围为 $\left(0,\dfrac 14\right]$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2