如图，$ABEDFC$ 为多面体，平面 $ABED$ 与平面 $ACFD$ 垂直，点 $O$ 在线段 $AD$ 上，$OA = 1$，$OD = 2$，$\triangle OAB $，$\triangle OAC$，$\triangle ODE$，$\triangle ODF$ 都是正三角形．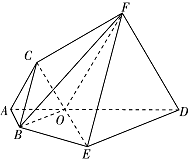
【难度】
【出处】
无
【标注】
-
证明直线 $BC\parallel EF$；标注答案解析设 $G$ 是线段 $DA$ 延长线与线段 $EB$ 延长线的交点．
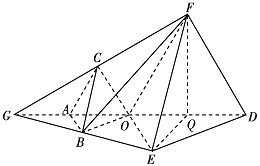由于 $\triangle OAB$ 与 $\triangle ODE$ 都是正三角形，所以 $OB \parallel DE$，\[OB = \dfrac{1}{2}DE,OG = OD = 2.\]同理，设 $G'$ 是线段 $DA$ 延长线与线段 $FC$ 延长线的交点，有\[OG' = OD = 2.\]又由于 $G$ 和 $G'$ 都在线段 $DA$ 的延长线上，所以 $G$ 与 $G'$ 重合．
在 $\triangle GED$ 和 $\triangle GFD$ 中，由 $OB \parallel DE$，$OB = \dfrac{1}{2}DE$ 和 $OC \parallel DF$，$OC =\dfrac{1}{2}DF$，
可知 $B$，$C$ 分别是 $GE$ 和 $GF$ 的中点，所以 $BC$ 是 $\triangle GEF$ 的中位线，故 $BC\parallel EF$． -
求棱锥 $F - OBED$ 的体积．标注答案解析由 $OB = 1$，$OE = 2$，$\angle EOB = 60^\circ $，知\[{S_{\triangle EOB}} = \dfrac{\sqrt 3 }{2},\]而 $\triangle OED$ 是边长为 $ 2 $ 的正三角形，故\[{S_{\triangle OED}} = \sqrt 3,\]所以\[{S_{四边形OBED}} = {S_{\triangle EOB}} + {S_{\triangle OED}} = \dfrac{3\sqrt 3 }{2}.\]过点 $F$ 作 $FQ \perp AD$，交 $AD$ 于点 $Q$，由平面 $ABED \perp 平面 ACFD$ 知，
$FQ$ 就是四棱锥 $F - OBED$ 的高，且 $FQ = \sqrt 3 $，所以\[{V_{F - OBED}} = \dfrac{1}{3}FQ \cdot {S_{四边形OBED}} = \dfrac{3}{2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
