已知平面上的线段 $l$ 及点 $P$，在 $l$ 上任取一点 $Q$，线段 $PQ$ 长度的最小值称为点 $P$ 到线段 $l$ 的距离，记作 $d\left(P,l\right)$．
【难度】
【出处】
无
【标注】
-
求点 $P\left(1,1\right)$ 到线段 $l:x - y - 3 = 0$ $\left(3 \leqslant x \leqslant 5\right)$ 的距离 $d\left(P,l\right)$；标注答案解析设 $Q\left(x,x - 3\right)$ 是线段 $l:x - y - 3 = 0$ $\left(3 \leqslant x \leqslant 5\right)$ 上一点，则\[\left| {PQ} \right| = \sqrt {{{\left(x - 1\right)}^2} + {{\left(x - 4\right)}^2}} = \sqrt {2{{\left( {x - \dfrac{5}{2}} \right)}^2} + \dfrac{9}{2}} \left(3 \leqslant x \leqslant 5\right),\]当 $x = 3$ 时，\[d\left(P,l\right) = |PQ{|_{\min }} = \sqrt 5 .\]
-
设 $l$ 是长为 $ 2 $ 的线段，求点的集合 $D = \left\{ P\left| d\left(P,l\right) \leqslant 1\right\} \right.$ 所表示的图形面积；标注答案解析设线段 $l$ 的端点分别为 $A$，$B$，以直线 $AB$ 为 $x$ 轴，$AB$ 的中点为原点建立直角坐标系．如图．
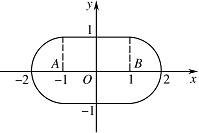则 $A\left( - 1,0\right)$，$B\left(1,0\right)$，点集 $D$ 由如下曲线围成\[\begin{split} {l_1}&:y = 1\left( {\left| x \right| \leqslant 1} \right), \\ {l_2}&:y = - 1\left( {\left| x \right| \leqslant 1} \right) , \\ {C_1}&:{\left(x + 1\right)^2} + {y^2} = 1\left(x \leqslant - 1\right) , \\ {C_2}&:{\left(x - 1\right)^2} + {y^2} = 1\left(x \geqslant 1\right) ,\end{split} \]其面积为\[S = 4 + {\mathrm \pi } .\] -
写出到两条线段 ${l_1}$，${l_2}$ 距离相等的点的集合 $\Omega = \left\{ P\left| d\left(P,{l_1}\right) = d\left(P,{l_2}\right)\right\} \right.$，其中 ${l_1} = AB$，${l_2} = CD$，$A$，$B$，$C$，$D$ 是下列三组点中的一组．对于下列三组点只需选做一种，满分分别是 ① $ 2 $ 分，② $ 6 $ 分，③ $ 8 $ 分；若选择了多于一种情形，则按照序号较小的解答计分．
① $A\left(1,3\right)$，$B\left(1,0\right)$，$C\left( - 1,3\right)$，$D\left( - 1,0\right)$．
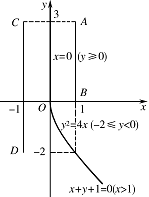
② $A\left(1,3\right)$，$B\left(1,0\right)$，$C\left( - 1,3\right)$，$D\left( - 1, - 2\right)$．
③ $A\left(0,1\right)$，$B\left(0,0\right)$，$C\left(0,0\right)$，$D\left(2,0\right)$．标注答案解析① 选择 $A\left(1,3\right)$，$B\left(1,0\right)$，$C\left( - 1,3\right)$，$D\left( - 1,0\right)$．如图．\[\Omega = \left\{ \left(x,y\right) \left|\right. x = 0\right\} ;\]② 选择 $A\left(1,3\right)$，$B\left(1,0\right)$，$C\left( - 1,3\right)$，$D\left( - 1, - 2\right)$．如图．\[\begin{split}\Omega &= \left\{ \left(x,y\right) \left|\right. x = 0,y \geqslant 0\right\} \\& \cup \left\{ \left(x,y\right)\left| {y^2} = 4x, - 2 \leqslant y < 0\right.\right\}\\ &\cup \left\{ \left(x,y\right) \left|\right. x + y + 1 = 0,x > 1\right\};\end{split}\]③ 选择 $A\left(0,1\right)$，$B\left(0,0\right)$，$C\left(0,0\right)$，$D\left(2,0\right)$．如图．\[\begin{split}\Omega &= \left\{ \left(x,y\right) \left|\right. x \leqslant 0,y \leqslant 0\right\} \\ &\cup \left\{ \left(x,y\right) \left|\right. y = x,0 < x \leqslant 1\right\} \\ &\cup \left\{ \left(x,y\right) \left|\right. {x^2} = 2y - 1,1 < x \leqslant 2\right\} \\ &\cup \left\{ \left(x,y\right) \left|\right. 4x - 2y - 3 = 0,x > 2\right\} .\end{split}\]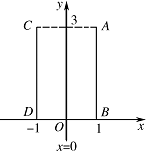
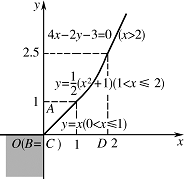
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
