如图,已知四棱锥 $P - ABCD$ 的底面为等腰梯形,$AB \parallel CD$,$AC \perp BD$,垂足为 $H$,$PH$ 是四棱锥的高.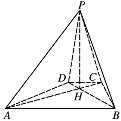

【难度】
【出处】
2010年高考新课标全国卷(文)
【标注】
-
证明:平面 $PAC \perp 平面 PBD$;标注答案解析因为 $ PH $ 是四棱锥 $ P-ABCD $ 的高,所以 $AC \perp PH$.
又 $ AC \perp BD$,$ PH $,$ BD $ 都在平面 $ PBD $ 内,且 $PH \cap BD=H$.
所以 $AC \perp 平面 PBD $.
故 $ 平面 PAC \perp 平面 PBD $. -
若 $AB = \sqrt 6 $,$\angle APB = \angle ADB = 60^\circ $,求四棱锥 $P - ABCD$ 的体积.标注答案解析因为 $ ABCD $ 为等腰梯形,$AB \parallel CD$,$AC \perp BD$,$AB= \sqrt 6 $.
所以\[HA=HB= \sqrt 3 .\]因为\[\angle APB= \angle ADB=60^\circ,\]所以\[PA=PB= \sqrt 6 ,HD=HC=1.\]可得\[PH= \sqrt 3 .\]等腰梯形 $ ABCD $ 的面积为\[S= \dfrac{1}{2} AC \times BD = 2+ \sqrt 3 . \]所以四棱锥的体积为\[V= \dfrac{1}{3} \times \left(2+ \sqrt 3 \right) \times \sqrt 3 = \dfrac{3 + 2\sqrt 3 }{3}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2