如图，在五面体 $ ABCDEF $ 中，四边形 $ ADEF $ 是正方形，$ FA\perp 平面 ABCD $，$ BC\parallel AD $，$ CD=1 $，$ AD= 2 \sqrt 2$，$ \angle BAD=\angle CDA=45^\circ $．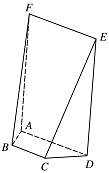
【难度】
【出处】
2010年高考天津卷（文）
【标注】
-
求异面直线 $ CE $ 与 $ AF $ 所成角的余弦值；标注答案解析因为四边形 $ ADEF $ 是正方形，所以 $ FA\parallel ED $，则 $\angle CED$ 为异面直线 $ CE $ 与 $ AF $ 所成的角．
因为 $FA \perp 平面 ABCD$，所以 $FA \perp CD$，从而 $ ED \perp CD $．
在 $ {\mathrm{Rt}}\triangle CDE $ 中，\[ CE= \sqrt {C{D^2} + E{D^2}} =3 ,\]所以\[\cos \angle CED = \dfrac{{ED}}{{CE}} = \dfrac{{2\sqrt 2 }}{3} .\]故异面直线 $ CE $ 和 $ AF $ 所成角的余弦值为 $\dfrac{{2\sqrt 2 }}{3}$． -
证明 $ CD\perp 平面 ABF $；标注答案解析过点 $ B $ 作 $ BG\parallel CD $，交 $ AD $ 于点 $ G $，
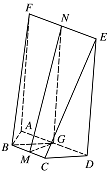则 $\angle BGA = \angle CDA = {45^ \circ }$．
由 $\angle BAD = {45^ \circ }$，可得 $ BG \perp AB $，
从而 $ CD \perp AB $，
又 $ CD \bot FA $，$ FA \cap AB=A $，
所以 $ CD \bot 平面 ABF $． -
求二面角 $ B-EF-A $ 的正切值．标注答案解析由（2）及已知，可得 $ AG= \sqrt 2 $，即 $ G $ 为 $ AD $ 的中点．
取 $ EF $ 的中点 $ N $，连接 $ GN $，则 $ GN \perp EF $，
因为 $ BC\parallel AD $，所以 $ BC\parallel EF $．
过点 $ N $ 作 $ NM \perp EF $，交 $ BC $ 于 $ M $，则 $\angle GNM$ 为二面角 $ B-EF-A $ 的平面角．
连接 $ GM $，可得 $ AD \perp 平面 GNM $，则 $AD \perp GM$，从而 $BC \perp GM$．
由已知，可得 $GM= \dfrac{{\sqrt 2 }}{2}$．
由 $NG\parallel FA$，$FA \perp GM$，得 $NG \perp GM$．
在 $ {\mathrm{Rt}}\triangle NGM $ 中，\[\tan \angle GNM = \dfrac{{{{GM}}}}{{{{NG}}}} = \dfrac{1}{{{4}}},\]所以二面角 $ B-EF-A $ 的正切值为 $\dfrac{1}{{{4}}}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
