如图,直三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,$AC = BC$,$A{A_1} = AB$,$D$ 为 $B{B_1}$ 的中点,$E$ 为 $A{B_1}$ 上的一点,$AE = 3E{B_1}$.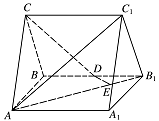

【难度】
【出处】
无
【标注】
-
证明:$DE$ 为异面直线 $A{B_1}$ 与 $CD$ 的公垂线;标注答案解析法一:如图,连接 ${A_1}B$,记 ${A_1}B$ 与 $A{B_1}$ 的交点为 $ F $.
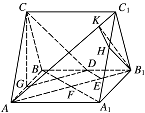 因为面 $A{A_1}{B_1}B$ 为正方形,故 ${A_1}B \perp A{B_1}$,且 $AF = F{B_1}$.
因为面 $A{A_1}{B_1}B$ 为正方形,故 ${A_1}B \perp A{B_1}$,且 $AF = F{B_1}$.
又 $AE = 3E{B_1}$,所以 $FE = E{B_1}$,又 $ D $ 为 $B{B_1}$ 的中点,
故 $DE\parallel BF$,$DE \perp A{B_1}$.
作 $CG \perp AB$,$ G $ 为垂足,由 $AC = BC$ 知,$ G $ 为 $ AB $ 中点.
又由底面 $ABC \perp 面 A{A_1}{B_1}B$,得 $CG \perp 面 A{A_1}{B_1}B$.
连接 $ DG $,则 $DG \parallel A{B_1}$,故 $DE \perp DG$,易得 $DE \perp CD$.
所以 $ DE $ 为异面直线 $A{B_1}$ 与 $ CD $ 的公垂线.
法二:以 $B$ 为坐标原点,射线 $ BA $ 为 $ x $ 轴正半轴,射线 $ BB_1 $ 为 $ y $ 轴正半轴,建立如图所示的空间直角坐标系 $ B-xyz $.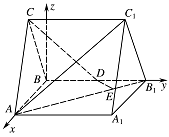 设 $ AB=2 $,则\[A\left(2,0,0\right) , B_1\left(0,2,0\right) ,D\left(0,1,0\right), E\left(\dfrac 1 2 ,\dfrac 3 2 ,0\right).\]又设 $ C\left(1,0,c\right)$,则\[\overrightarrow {DE} =\left(\dfrac 1 2 ,\dfrac 1 2 ,0\right),\overrightarrow {B_1A} =\left(2,-2,0\right),\overrightarrow {DC} =\left(1,-1,c\right). \]于是 $ \overrightarrow {DE} \cdot \overrightarrow {B_1A} =0 $,$\overrightarrow {DE} \cdot \overrightarrow {DC} =0 $,故 $ \overrightarrow {DE} \perp \overrightarrow {B_1A} $,$ \overrightarrow {DE} \perp \overrightarrow {DC} $.
设 $ AB=2 $,则\[A\left(2,0,0\right) , B_1\left(0,2,0\right) ,D\left(0,1,0\right), E\left(\dfrac 1 2 ,\dfrac 3 2 ,0\right).\]又设 $ C\left(1,0,c\right)$,则\[\overrightarrow {DE} =\left(\dfrac 1 2 ,\dfrac 1 2 ,0\right),\overrightarrow {B_1A} =\left(2,-2,0\right),\overrightarrow {DC} =\left(1,-1,c\right). \]于是 $ \overrightarrow {DE} \cdot \overrightarrow {B_1A} =0 $,$\overrightarrow {DE} \cdot \overrightarrow {DC} =0 $,故 $ \overrightarrow {DE} \perp \overrightarrow {B_1A} $,$ \overrightarrow {DE} \perp \overrightarrow {DC} $.
所以 $ DE $ 为异面直线 $ AB_1 $ 与 $ CD $ 的公垂线. -
设异面直线 $A{B_1}$ 与 $CD$ 的夹角为 $ 45^\circ $,求二面角 ${A_1} - A{C_1} - {B_1}$ 的大小.标注答案解析解法一:因为 $DG\parallel A{B_1}$,故 $\angle CDG$ 为异面直线 $A{B_1}$ 与 $ CD $ 的夹角,$\angle CDG = {45^ \circ }$.
设 $AB = 2$,则\[A{B_1} = 2\sqrt 2 ,DG = \sqrt 2 ,CG = \sqrt 2 ,AC = \sqrt 3 .\]如图,作 ${B_1}H \perp {A_1}{C_1}$,$ H $ 为垂足.因为底面 ${A_1}{B_1}{C_1} \perp 面 A{A_1}{C_1}C$,故 ${B_1}H \perp 面 A{A_1}{C_1}C$,又作 $HK \perp A{C_1}$,$ K $ 为垂足,连接 ${B_1}K$,易得 ${B_1}K \perp A{C_1}$,因此 $\angle {B_1}KH$ 为二面角 ${A_1} - A{C_1} - {B_1}$ 的平面角.
又\[ {B_1}H = \dfrac{{{A_1}{B_1} \times \sqrt {{A_1}C_1^2 - {{\left(\dfrac{1}{2}{A_1}{B_1}\right)}^2}} }}{{{A_1}{C_1}}} = \dfrac{{2\sqrt 2 }}{{\sqrt 3 }} ,
H{C_1} = \sqrt {{B_1}C_1^2 - {B_1}{H^2}} = \dfrac{{\sqrt 3 }}{3} , \\ A{C_1} = \sqrt {{2^2} + {{\left(\sqrt 3 \right)}^2}} = \sqrt 7 , HK = \dfrac{{A{A_1} \times H{C_1}}}{{A{C_1}}} = \dfrac{{2\sqrt 3 }}{{3\sqrt 7 }} ,\]所以 $\tan \angle B_1KH = \dfrac {B_1H}{HK} = \sqrt {14}$,所以二面角 ${A_1} - A{C_1} - {B_1}$ 的大小为 $\arctan \sqrt {14} $.
解法二:因为 $\left\langle {\overrightarrow {{B_1}A} ,\overrightarrow {DC} } \right\rangle $ 等于异面直线 $A{B_1}$ 与 $ CD $ 的夹角,故\[ \overrightarrow {{B_1}A} \cdot \overrightarrow {DC} = \left| {\overrightarrow {{B_1}A} } \right| \cdot \left| {\overrightarrow {DC} } \right|\cos {45^ \circ } ,\]即\[2\sqrt 2 \times \sqrt {{c^2} + 2} \times \dfrac{{\sqrt 2 }}{2} = 4,\]解得 $c = \sqrt 2 $,故 $\overrightarrow {AC} = \left( - 1,0,\sqrt 2 \right)$.
又 $\overrightarrow {A{A_1}} = \overrightarrow {B{B_1}} = \left(0,2,0\right)$,所以\[\overrightarrow {A{C_1}} = \overrightarrow {AC} + \overrightarrow {A{A_1}} = \left( - 1,2,\sqrt 2 \right) .\]设平面 $A{A_1}{C_1}$ 的法向量为 $\overrightarrow m = \left(x,y,z\right)$,则\[ \overrightarrow m \cdot \overrightarrow {A{C_1}} = 0,\overrightarrow m \cdot \overrightarrow {A{A_1}} = 0 ,\]即\[ - x + 2y + \sqrt 2 z = 0 , 2y = 0 .\]令 $x = \sqrt 2 $,则 $z = 1,y = 0$,故 $\overrightarrow m = \left(\sqrt 2 ,0,1\right)$.
设平面 $A{B_1}{C_1}$ 的法向量为 $\overrightarrow n = \left(p,q,r\right)$,则\[\overrightarrow n \cdot \overrightarrow {A{C_1}} = 0,\overrightarrow n \cdot \overrightarrow {{B_1}A} = 0 ,\]即\[- p + 2q + \sqrt 2 r = 0,2p - 2q = 0 .\]令 $p = \sqrt 2 $,则 $q = \sqrt 2 ,r = - 1$,故 $\overrightarrow n = \left(\sqrt 2 ,\sqrt 2 , - 1\right)$.
所以\[ \cos \left\langle {\overrightarrow m,\overrightarrow n} \right\rangle = \dfrac{{\overrightarrow m \cdot \overrightarrow n}}{{\left|\overrightarrow m \right|\left| \overrightarrow n \right|}} = \dfrac{1}{{\sqrt {15} }} .\]由于 $\left\langle {\overrightarrow m,\overrightarrow n} \right\rangle $ 等于二面角 ${A_1} - A{C_1} - {B_1}$ 的平面角,所以二面角 ${A_1} - A{C_1} - {B_1}$ 的大小为 $\arccos \dfrac{{\sqrt {15} }}{{15}}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2