某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的 $ 40 $ 件产品作为样本称出它们的重量(单位:克),重量的分组区间为 $ \left(490,495\right],\left(495,500\right],\cdots,\left(510,515\right] $,由此得到样本的频率分布直方图,如图所示.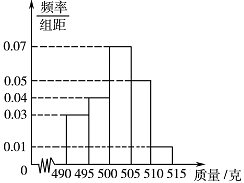

【难度】
【出处】
2010年高考广东卷(理)
【标注】
-
根据频率分布直方图,求重量超过 $ 505 $ 克的产品数量.标注答案解析重量超过 $ 505 $ 克的产品数量是\[40 \times \left(0.05 \times 5 + 0.01 \times 5\right) = 12 件.\]
-
在上述抽取的 $ 40 $ 件产品中任取 $ 2 $ 件,设 $ Y $ 为重量超过 $ 505 $ 克的产品数量,求 $ Y $ 的分布列.标注答案解析依题意 $ Y $ 的所有可能取值为 $ 0,1,2 $.\[\begin{split}P\left(Y = 0\right) &= \dfrac{{{\mathrm{C}}_{28}^2}}{{{\mathrm{C}}_{40}^2}} = \dfrac{63}{130},\\ P\left(Y = 1\right) &= \dfrac{{ {\mathrm{C }}_{12}^1{\mathrm{C}}_{28}^1}}{{{\mathrm{C}}_{40}^2}} = \dfrac{28}{65},\\P\left(Y = 2\right) &= \dfrac{{{\mathrm{C}}_{12}^2}}{{{\mathrm{C}}_{40}^2}} = \dfrac{11}{130},\end{split}\]所以 $Y $ 的分布列为\[\begin{array}{|c|c|c|c|}\hline
Y&0&1&2\\ \hline
P&\dfrac{63}{130}&\dfrac{28}{65}&\dfrac{11}{130}\\ \hline
\end{array}\] -
从流水线上任取 $ 5 $ 件产品,求恰有 $ 2 $ 件产品合格的重量超过 $ 505 $ 克的概率.标注答案解析该流水线上产品重量超过 $ 505 $ 克的概率为 $ 0.3 $.
令 $ \xi$ 为任取的 $ 5 $ 件产品中重量超过 $ 505 $ 克的产品数量,则 $\xi~B\left(5,0.3\right) $,
故所求的概率为\[P\left( {\xi = 2} \right) = {\mathrm{C}}_5^2{\left( {0.3} \right)^2}\left( 1-{0.3} \right)^3 = 0.3087.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3