如图,$\overparen {AEC}$ 是半径为 $a$ 的半圆,$AC$ 为直径,点 $E$ 为 $\overparen {AC}$ 的中点,点 $B$ 和点 $C$ 为线段 $AD$ 的三等分点,平面 $AEC$ 外一点 $F$ 满足 $FB = FD = \sqrt 5 a$,$EF = \sqrt 6 a$.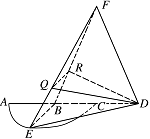

【难度】
【出处】
2010年高考广东卷(理)
【标注】
-
证明:$EB \perp FD$;标注答案解析$\because$ $ E$ 为 $\overparen {AC}$ 的中点,$AB=BC $,$AC$ 为直径,
$\therefore$ $EB \perp AD$.
$\because$ $EF^2=6a^2=\left(\sqrt5a\right)^2+a^2=BF^2+BE^2 $,
$\therefore$ $EB\perp FB $.
又 $\because$ $ BF\cap BD=B$,
$\therefore$ $ EB\perp平面BDF$.
$\because$ $FD\subset平面BDF $,
$\therefore$ $ EB\perp FD$. -
已知点 $Q,R$ 为线段 $FE,FB$ 上的点,$FQ = \dfrac{2}{3}FE$,$FR = \dfrac{2}{3}FB$,求平面 $BED$ 与平面 $RQD$ 所成二面角的正弦值.标注答案解析方法一:如图,过 $D $ 作 $ HD\parallel QR$.
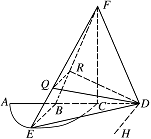 由 $FQ = \dfrac{2}{3}FE$,$FR = \dfrac{2}{3}FB$,知 $QR\parallel EB$,
由 $FQ = \dfrac{2}{3}FE$,$FR = \dfrac{2}{3}FB$,知 $QR\parallel EB$,
$\therefore$ $HD\parallel EB $.
又 $\because$ $ D\in平面 BED\cap平面 RQD$,
$\therefore$ $ HD$ 为平面 $BED $ 与平面 $RQD $ 的交线.
$\because$ $DR,DB \subset 平面 BDF$,$BE\perp 平面 BDF$,
$\therefore$ $HD\perp 平面 BDF $ 从而 $HD\perp BD $,$ HD\perp RD$,
则 $\angle RDB$ 是平面 $BED$ 与平面 $RQD$ 所成二面角的平面角.
由 $FB=FD $,$BC=CD $,得 $ FC\perp BD$,则\[\cos \angle FBC = \dfrac{{BC}}{{BF}} = \dfrac{{a}}{{\sqrt 5 a}} = \dfrac{{\sqrt 5 }}5,\]从而\[\sin \angle FBC = \dfrac{2\sqrt 5 }5,\]由余弦定理得\[\begin{split}RD &= \sqrt {B{D^2} + B{R^2} - 2BD \cdot BR\cos \angle RBD} \\&= \sqrt {{{\left(2a\right)}^2} + {{\left(\dfrac{{\sqrt 5 a}}{3}\right)}^2} - 2 \cdot 2a \cdot \dfrac{{\sqrt 5 a}}{3} \cdot \dfrac{1}{{\sqrt 5 }}} \\&= \dfrac{{\sqrt {29} }}{3}a .\end{split}\]由正弦定理得\[\begin{split}\sin \angle RDB& =\dfrac{RB}{RD}\cdot \sin \angle FBC\\&=\dfrac{\dfrac{\sqrt3}a}{\dfrac{\sqrt{29}}3a}\cdot\dfrac2{\sqrt5}= \dfrac{{2\sqrt {29} }}{{29}}.\end{split}\]故平面 $ BED$ 与平面 $RQD $ 所成二面角正弦值为 $ \dfrac{2\sqrt{29}}{29}$.
方法 二:
如图,以 $B $ 为原点,$ \overrightarrow {BE}$ 为 $x$ 轴正方向,$\overrightarrow {BD} $ 为 $y $ 轴正方向,过 $ B$ 作平面 $ BEC$ 的垂线,建立空间直角坐标系,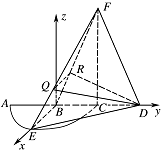 由此得 $B\left(0,0,0\right) $,$C\left(0,a,0\right) $,$D\left(0,2a,0\right) $,$E\left(a,0,0\right) $,
由此得 $B\left(0,0,0\right) $,$C\left(0,a,0\right) $,$D\left(0,2a,0\right) $,$E\left(a,0,0\right) $,
由 $FD=FB $,$BC=CD $,得 $ FC\perp BD$,则 $ FC=2a$.
由 $ FQ=\dfrac23FE$,$ FR=\dfrac23FB$,得\[R\left(0,\dfrac13a,\dfrac23a\right),\]从而\[\begin{split}\overrightarrow {RQ}&=\dfrac23\overrightarrow {BE}=\left(\dfrac23a,0,0\right),\\ \overrightarrow {RD}&=\left(0,\dfrac53a,-\dfrac23a\right) .\end{split}\]设平面 $ RQD$ 的法向量为 $ \overrightarrow {n_1}=\left(x,y,z\right)$,则\[ \begin{cases}\overrightarrow {n_1}\cdot\overrightarrow {RD}=0, \\ \overrightarrow {n_1}\cdot\overrightarrow {RQ}=0,\end{cases}\]即\[ \begin{cases}ax=0,\\ 5ay-2az=0,\end{cases}\]所以\[ \overrightarrow {n_1}=\left(0,2,5\right),\]而平面 $BED $ 的法向量为 $\overrightarrow {n_2} =\left(0,0,1\right)$,所以\[\cos \left\langle\overrightarrow {n_1}\cdot\overrightarrow {n_2} \right\rangle=\dfrac{5\sqrt{29}}{29},\]从而\[\sin \left\langle\overrightarrow {n_1}\cdot\overrightarrow {n_2} \right\rangle=\dfrac{2\sqrt{29}}{29} .\]故平面 $ BED$ 与平面 $RQD $ 所成二面角正弦值为 $ \dfrac{2\sqrt{29}}{29}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2