如图,圆柱 $ O O _ 1 $ 内有一个三棱柱 $ ABC - A _ 1 B _ 1 C _ 1 $,三棱柱的底面为圆柱底面的内接三角形,且 $ AB $ 是圆 $ O $ 直径.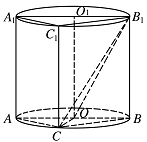

【难度】
【出处】
2010年高考福建卷(理)
【标注】
-
证明:$ 平面 A _1 AC C _1 \perp 平面 B _ 1 BC C _ 1 $;标注答案解析因为 $A{A_1} \perp 平面 ABC$,$BC \subset 平面 ABC$,所以 $A{A_1} \perp BC$.
因为 $ AB $ 是圆 $ O $ 直径,所以 $BC \perp AC$.
又 $AC \cap A{A_1} = A$,所以 $BC \perp 平面 {A_1}AC{C_1}$.
而 $BC \subset 平面 B_1BCC_1$,所以 $平面 {A_1}AC{C_1} \perp 平面 {B_1}BC{C_1}$. -
设 $ AB= AA_1$,在圆柱 $OO_1$ 内随机选取一点,记该点取自于三棱柱 $ABC - A_1B_1C_1$ 内的概率为 $p$.
(i)当点 $ C $ 在圆周上运动时,求 $p$ 的最大值;
(ii)记平面 ${ A _ 1}AC{C_1}$ 与平面 ${B_1}OC$ 所成的角为 $\theta \left({0^ \circ } < \theta \leqslant {90^ \circ }\right)$,当 $p$ 取最大值时,求 $\cos \theta $ 的值.标注答案解析(i)设圆柱的底面半径为 $r$,则 $ AB= AA_1=2r$,故三棱柱 $ ABC - A _ 1 B _ 1 C _ 1 $ 的体积为\[ V_1=\dfrac 1 2 AC\cdot BC \cdot 2r =AC \cdot BC \cdot r, \]又因为\[ A C ^2 + B C ^2 =AB^2=4r^2 ,\]所以\[AC \cdot BC \leqslant \dfrac {AC^2 +BC^2} 2 =2r^2,\]当且仅当 $AC = BC = \sqrt 2 r$ 时,\[{ V _1} \leqslant 2 r ^3.\]而圆柱的体积\[V =\pi r^2 \cdot 2r = 2\pi r^3 ,\]则有\[p = \dfrac{V_1}{V} \leqslant \dfrac{2r^3}{2\pi r^3}= \dfrac{1}{\pi },\]因此,当且仅当 $AC = BC = \sqrt 2 {{r}}$,即 ${{OC}} \perp {{AB}}$ 时,$p$ 的最大值是 $\dfrac{1}{\pi }$.
(ii)由(i)可知,$p$ 取最大值时,${{OC}} \perp {{AB}}$,于是以 $ O $ 为坐标原点,建立空间直角坐标系 ${{O - xyz}}$(如图),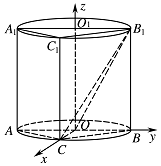 则\[C\left(r,0,0\right),B\left(0,r,0\right), {{{B}}_{{1}}} \left(0,r,2r\right),\]因为 ${{BC}} \perp 平面 {{{A}}_{{1}}}{{AC}}{{{C}}_{{1}}}$,所以 $\overrightarrow {{{BC}}} {{ = \left(r, - r,0\right)}}$ 是平面 ${{{A}}_{{1}}}{{AC}}{{{C}}_{{1}}}$ 的一个法向量.
则\[C\left(r,0,0\right),B\left(0,r,0\right), {{{B}}_{{1}}} \left(0,r,2r\right),\]因为 ${{BC}} \perp 平面 {{{A}}_{{1}}}{{AC}}{{{C}}_{{1}}}$,所以 $\overrightarrow {{{BC}}} {{ = \left(r, - r,0\right)}}$ 是平面 ${{{A}}_{{1}}}{{AC}}{{{C}}_{{1}}}$ 的一个法向量.
设平面 ${B_1}OC$ 的法向量为 $\overrightarrow {{n}} {{ = \left(x,y,z\right)}}$,由\[\begin{cases}
\overrightarrow {{n}} \bot \overrightarrow {{{OC}}}, \\
\overrightarrow {{n}} \bot \overrightarrow {{{O}}{{{B}}_{{1}}}}, \\
\end{cases}\]得\[\begin{cases}rx = 0 ,\\
ry + 2rz = 0, \\
\end{cases}\]取 $z = 1$ 得平面 ${B_1}OC$ 的一个法向量为\[\overrightarrow {{n}} {{ = \left(0, - 2,1\right)}},\]因为 ${0^ \circ }{{ < }}\theta \leqslant {90^ \circ }$,所以\[ \cos \theta = \left|\cos \left\langle {\overrightarrow n ,\overrightarrow {{{BC}}} } \right\rangle \right| = \left| {\dfrac{{\overrightarrow n \cdot \overrightarrow {BC} }}{{ \left|\overrightarrow n \right| \cdot \left|\overrightarrow {BC} \right|}}} \right| = \left| {\dfrac{{2r}}{{\sqrt 5 \times \sqrt 2 r}}} \right| = \dfrac{{\sqrt {10} }}{5} .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2