如图,四棱锥 $ S-ABCD $ 中,$ SD \perp 底面 ABCD $,$ AB\parallel DC $,$ AD \perp DC $,$ AB=AD=1 $,$ DC=SD=2 $,$ E $ 为棱 $ SB $ 上的一点,$ 平面 EDC \perp 平面 SBC $.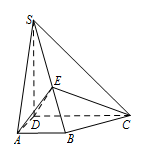

【难度】
【出处】
无
【标注】
-
证明:$ SE=2EB $;标注答案解析法一:
连接 $ BD $,取 $ DC $ 的中点 $ G $,连接 $ BG $,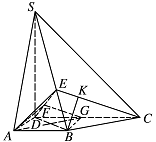 由此知 $DG=GC=BG=1$,
由此知 $DG=GC=BG=1$,
即 $\triangle DBC$ 为直角三角形,故 $BC\perp BD$.
又 $SD\perp 平面 {ABCD } $,故 $ {BC}\perp {SD}$,
所以,$ BC\perp 平面 BDS$,$BC\perp DE$.
作 $BK\perp EC$,$K$ 为垂足,因 $平面 EDC\perp 平面 SBC$,
故 $BK\perp 平面 EDC$,$BK\perp DE$,$DE$ 与平面 $SBC$ 内的两条相交直线 $BK$、$BC$ 都垂直,
$DE\perp 平面 SBC$,$DE\perp EC$,$DE\perp SB$.
又\[ SB=\sqrt{S{{D}^{2}}+D{{B}^{2}}}=\sqrt{6}, DE=\frac{SD\centerdot DB}{SB}=\frac{2}{\sqrt{3}},\\
EB=\sqrt{D{{B}^{2}}-D{{E}^{2}}}=\frac{\sqrt{6}}{3},SE=SB-EB=\frac{2\sqrt{6}}{3},\]所以,$SE=2EB$.
法二:
以 $ D $ 为坐标原点,射线 $ DA $,$DC $,$DS $ 分别为 $ x $ 轴,$ y$ 轴,$z $ 轴的正半轴,建立如图所示的直角坐标系 $ D-xyz $,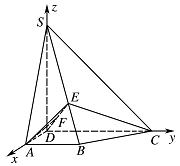 设 $ A\left(1,0,0\right) $,则 $ B\left(1,1,0\right)$,$C\left(0,2,0\right)$,$S\left(0,0,2\right)$,所以\[\overrightarrow {SC} = \left(0,2, - 2\right),\overrightarrow {BC} = \left( - 1,1,0\right).\]设平面 $ SBC $ 的法向量为 $ \overrightarrow n =\left(a,b,c\right)$,由\[\overrightarrow n \perp \overrightarrow {SC} ,\overrightarrow n \perp \overrightarrow {BC} ,\]得\[\overrightarrow n \cdot \overrightarrow {SC} = 0,\overrightarrow n \cdot \overrightarrow {BC} = 0, \]故\[2b-2c=0,-a+b=0.\]令 $ a=1 $,则\[b=1 , c=1 , \overrightarrow n =\left(1,1,1\right) .\]又设 $\overrightarrow {SE} = \lambda \overrightarrow {EB} $ $\left(\lambda > 0\right)$,则\[E\left(\dfrac{\lambda }{{1 + \lambda }},\dfrac{\lambda }{{1 + \lambda }},\dfrac{2}{{1 + \lambda }}\right), \overrightarrow {DE} = \left(\dfrac{\lambda }{{1 + \lambda }},\dfrac{\lambda }{{1 + \lambda }},\dfrac{2}{{1 + \lambda }}\right),\overrightarrow {DC} = \left(0,2,0\right) . \]设平面 $ CDE $ 的法向量 $\overrightarrow m =\left(x,y,z\right)$,由 $ \overrightarrow m \perp \overrightarrow {DE}$,$\overrightarrow m \perp \overrightarrow {DC} $,得\[\overrightarrow m \cdot \overrightarrow {DE} = 0 , \overrightarrow m \cdot \overrightarrow {DC} = 0,\]故\[ \dfrac{{\lambda x}}{{1 + \lambda }} + \dfrac{{\lambda y}}{{1 + \lambda }} + \dfrac{{2z}}{{1 + \lambda }} = 0,2y = 0 .\]令 $x = 2$,则 $\overrightarrow m = \left(2,0, - \lambda \right)$.由 $ 平面 DEC\perp 平面 SBC $,得 $\overrightarrow m \perp \overrightarrow n$,所以\[\overrightarrow m \cdot \overrightarrow n = 0,2 - \lambda = 0,\lambda = 2.\]故 $ SE=2EB $.
设 $ A\left(1,0,0\right) $,则 $ B\left(1,1,0\right)$,$C\left(0,2,0\right)$,$S\left(0,0,2\right)$,所以\[\overrightarrow {SC} = \left(0,2, - 2\right),\overrightarrow {BC} = \left( - 1,1,0\right).\]设平面 $ SBC $ 的法向量为 $ \overrightarrow n =\left(a,b,c\right)$,由\[\overrightarrow n \perp \overrightarrow {SC} ,\overrightarrow n \perp \overrightarrow {BC} ,\]得\[\overrightarrow n \cdot \overrightarrow {SC} = 0,\overrightarrow n \cdot \overrightarrow {BC} = 0, \]故\[2b-2c=0,-a+b=0.\]令 $ a=1 $,则\[b=1 , c=1 , \overrightarrow n =\left(1,1,1\right) .\]又设 $\overrightarrow {SE} = \lambda \overrightarrow {EB} $ $\left(\lambda > 0\right)$,则\[E\left(\dfrac{\lambda }{{1 + \lambda }},\dfrac{\lambda }{{1 + \lambda }},\dfrac{2}{{1 + \lambda }}\right), \overrightarrow {DE} = \left(\dfrac{\lambda }{{1 + \lambda }},\dfrac{\lambda }{{1 + \lambda }},\dfrac{2}{{1 + \lambda }}\right),\overrightarrow {DC} = \left(0,2,0\right) . \]设平面 $ CDE $ 的法向量 $\overrightarrow m =\left(x,y,z\right)$,由 $ \overrightarrow m \perp \overrightarrow {DE}$,$\overrightarrow m \perp \overrightarrow {DC} $,得\[\overrightarrow m \cdot \overrightarrow {DE} = 0 , \overrightarrow m \cdot \overrightarrow {DC} = 0,\]故\[ \dfrac{{\lambda x}}{{1 + \lambda }} + \dfrac{{\lambda y}}{{1 + \lambda }} + \dfrac{{2z}}{{1 + \lambda }} = 0,2y = 0 .\]令 $x = 2$,则 $\overrightarrow m = \left(2,0, - \lambda \right)$.由 $ 平面 DEC\perp 平面 SBC $,得 $\overrightarrow m \perp \overrightarrow n$,所以\[\overrightarrow m \cdot \overrightarrow n = 0,2 - \lambda = 0,\lambda = 2.\]故 $ SE=2EB $. -
求二面角 $ A-DE-C $ 的大小.标注答案解析法一:
由 $SA=\sqrt{{SD}^2+{AD}^2}=\sqrt 5$,$AB=1$,$SE=2EB$,$AB \perp SA$,知\[AE=\sqrt{{{\left( \frac{1}{3}SA \right)}^{2}}+{{\left( \frac{2}{3}AB \right)}^{2}}}=1.\]又 $AD=1$,故 $ \triangle ADE $ 为等腰三角形.
如图,取 $ ED $ 中点 $ F $,连接 $ AF $,则\[AF\perp DE,AF=\sqrt{A{{D}^{2}}-D{{F}^{2}}}=\frac{\sqrt{6}}{3}.\]连接 $ FG $,则\[ FG\parallel EC,FG\perp DE. \]所 以,$ \angle AFG $ 是二面角 $ A-DE-C $ 的平面角.
连接 $ AG $,所以\[ A G= \sqrt{2} , FG=\sqrt{D{{G}^{2}}-D{{F}^{2}}}=\frac{\sqrt{6}}{3} ,\]所以\[ \cos \angle AFG=\frac{A{{F}^{2}}+F{{G}^{2}}-A{{G}^{2}}}{2\centerdot AF\centerdot FG}=-\frac{1}{2},\]所以,二面角 $ A-DE-C $ 的大小为 $ 120^\circ $.
法二:由(1)知 $E\left(\dfrac{2}{3},\dfrac{2}{3},\dfrac{2}{3}\right)$,取 $ DE $ 的中点 $ F $,则\[F\left(\dfrac{1}{3},\dfrac{1}{3},\dfrac{1}{3}\right),\overrightarrow {FA} = \left(\dfrac{2}{3}, - \dfrac{1}{3}, - \dfrac{1}{3}\right) ,\]故 $\overrightarrow {FA} \cdot \overrightarrow {DE} = 0$,由此得 $FA \perp DE$.
又 $\overrightarrow {EC} = \left( - \dfrac{2}{3},\dfrac{4}{3}, - \dfrac{2}{3}\right)$,故 $\overrightarrow {EC} \cdot \overrightarrow {DE} = 0$,由此得 $EC \perp DE$,
向量 $\overrightarrow {FA} $ 与 $\overrightarrow {EC} $ 的夹角等于二面角 $A - DE - C$ 的平面角.
于是\[\cos \left\langle \overrightarrow {FA} ,\overrightarrow {EC} \right\rangle = \dfrac{{\overrightarrow {FA} \cdot \overrightarrow {EC} }}{{\left|\overrightarrow {FA} \right|\left|\overrightarrow {EC} \right|}} = - \dfrac{1}{2}.\]所以,二面角 $A - DE - C$ 的大小为 ${120^ \circ }$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2