如图,在四棱锥 $ P-ABCD $ 中,$ PD\perp 平面 ABCD $,$ PD=DC=BC=1 $,$ AB=2 $,$ AB\parallel DC $,$ \angle BCD=90^\circ $.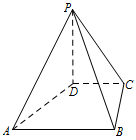

【难度】
【出处】
2010年高考江苏卷
【标注】
-
求证:$ PC\perp BC $;标注答案解析法一:
因为 $ PD\perp 平面 ABCD $,$BC \subset 平面 ABCD $,所以 $ PD\perp BC $.
因为 $ \angle BCD=90^\circ $,所以 $ CD\perp BC $.
又 $ PD \cap CD = D$,所以 $ BC\perp 平面 PCD $.
而 $PC \subset 平面 PCD $,所以 $ PC\perp BC $.
法二:
过点 $D$ 作 $DE \parallel BC $ 交 $AB $ 于 $ E $,则 $ E $ 为 $ AB $ 中点.
因为 $ PD \perp 平面 ABCD $,所以 $ PD\perp CD $,$ PD \perp DE $.
因为 $ \angle BCD=90^\circ$,所以 $ CD\perp BC $,所以 $ CD\perp DE $.
以 $ D $ 为坐标原点 $ O $,$ DE $ 为 $ x $ 轴,$ DC $ 为 $ y $ 轴,$ DP $ 为 $ z $ 轴,建立空间直角坐标系,如图,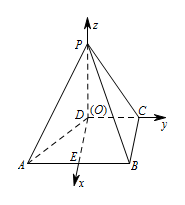 则\[ O\left(D\right)\left(0,0,0\right) , A\left(1,-1,0\right) , B\left(1,1,0\right) , C\left(0,1,0\right) , P\left(0,0,1\right). \]所以\[\overrightarrow {PC} = \left(0,1,-1\right) , \overrightarrow {BC} = \left(-1,0,0\right) ,\overrightarrow {PC} \cdot \overrightarrow {BC} =0, \]所以 $PC \perp BC $.
则\[ O\left(D\right)\left(0,0,0\right) , A\left(1,-1,0\right) , B\left(1,1,0\right) , C\left(0,1,0\right) , P\left(0,0,1\right). \]所以\[\overrightarrow {PC} = \left(0,1,-1\right) , \overrightarrow {BC} = \left(-1,0,0\right) ,\overrightarrow {PC} \cdot \overrightarrow {BC} =0, \]所以 $PC \perp BC $. -
求点 $ A $ 到平面 $ PBC $ 的距离.标注答案解析法一:
如图,过点 $ A $ 作 $ BC $ 的平行线交 $ CD $ 的延长线于 $ E $,过点 $ E $ 作 $ PC $ 的垂线,垂足为 $ F $,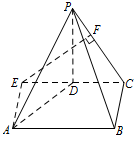 则有 $ AE\parallel 平面 PBC $,所以点 $ A $ 到平面 $ PBC $ 的距离等于点 $ E $ 到平面 $ PBC $ 的距离.
则有 $ AE\parallel 平面 PBC $,所以点 $ A $ 到平面 $ PBC $ 的距离等于点 $ E $ 到平面 $ PBC $ 的距离.
又 $ EF\perp PC $,$ BC\perp 平面 PCD $,则 $ EF\perp BC $.
而 $ BC\cap PC=C $,所以 $ EF\perp 平面 PBC $.$ EF $ 即为 $ E $ 到平面 $ PBC $ 的距离.
又因为 $ AE\parallel BC $,$ AB\parallel CD $,所以四边形 $ ABCE $ 为平行四边形.
所以 $ CE=AB=2 $.
又 $ PD=CD=1 $,$ PD\perp 平面 ABCD $,$ CD\subset 平面 ABCD $,
所以 $ PD\perp CD $,$ \angle PCD = 45^\circ $.
所以 $ EF= \sqrt 2 $,即点 $ A $ 到平面 $ PBC $ 的距离为 $ \sqrt 2 $.
法二:
设平面 $ PBC $ 的一个法向量为 $ \overrightarrow n =\left(x,y,z\right) $,点 $ A $ 到平面 $ PBC $ 的距离为 $ d $,则由\[ \overrightarrow n \perp \overrightarrow {PC} , \overrightarrow n \perp \overrightarrow {BC} ,\]得\[ \begin{cases}y-z=0 , \\ -x = 0 , \end{cases} \]解得\[ x=0,y=z. \]令 $ z=1 $,则 $ y=1 $,得\[ \overrightarrow n =\left(0,1,1\right) .\]又\[ \overrightarrow {PA} =\left(1,-1,-1\right) ,\]故\[ d = {\left|{\dfrac {\overrightarrow {PA} \cdot \overrightarrow n } {{\left|{\overrightarrow n }\right|}} }\right|} = \dfrac 2 {\sqrt 2} = \sqrt 2.\]所以点 $ A $ 到平面 $ PBC $ 的距离为 $ \sqrt 2 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2