某兴趣小组测量电视塔 $ AE $ 的高度 $ H $(单位:$ {\mathrm{m}} $),示意图如图所示,垂直放置的标杆 $ BC $ 高度 $ h=4 {\mathrm{m}} $,仰角 $ \angle ABE={\alpha} $,$ \angle ADE={\beta} $.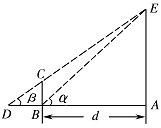

【难度】
【出处】
2010年高考江苏卷
【标注】
-
该小组已经测得一组 $ {\alpha} $、$ {\beta} $ 的值,$ \tan {\alpha} =1 .24$,$ \tan {\beta} =1.20 $,请据此算出 $ H $ 的值;标注答案解析因为\[\tan {\alpha} =\dfrac {AE} {AB} , \tan \beta =\dfrac {AE} {AD} ,\]所以\[ \dfrac {\tan \alpha} {\tan \beta} =\dfrac {AD} {AB} =\dfrac {31} {30} . \]又\[ \tan {\alpha} =\dfrac {H} {AB} , \tan \beta =\dfrac {4} {AD-AB} , \]所以\[\dfrac {H} {AB} \cdot \dfrac {AD-AB} {4} = \dfrac {AD} {AB} , \]把 $ \dfrac {AD} {AB} =\dfrac {31} {30} $ 代入得 $ H=124 {\mathrm{m}} $.
-
该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离 $ d $(单位:$ {\mathrm{m}} $),使 $ {\alpha} $ 与 $ {\beta} $ 之差较大,可以提高测量精确度,若电视塔实际高度为 $ 125 {\mathrm{m}} $,问 $ d $ 为多少时,$ {\alpha} -{\beta} $ 最大.标注答案解析由题设知 $ d=AB $,从而 $ \tan \alpha =\dfrac H d $.
由\[ AB=AD-BD =\dfrac H {\tan \beta} -\dfrac h {\tan \beta} ,\]得\[\tan \beta = \dfrac {H-h} d . \]所以\[ \tan \left(\alpha -\beta \right) =\dfrac {\tan \alpha - \tan \beta} {1+ \tan \alpha \tan \beta} =\dfrac h {d+\dfrac {H\left(H-h\right)} d } \leqslant \dfrac h {2\sqrt {H\left(H-h\right)}} ,\]当且仅当 $ d= \dfrac {H\left(H-h\right)} d $,即 $d= \sqrt {H\left(H-h\right)} = \sqrt{125 \times \left(125-4\right)} = 55\sqrt 5 $ 时,上式取等号.
所以当 $ d= 55\sqrt 5 $ 时,$ \tan \left(\alpha - \beta\right)$ 最大.
因为 $ 0 < \beta < \alpha < \dfrac {\rm{\pi}} 2 $,则 $ 0 < \alpha - \beta < \dfrac {\rm{\pi}} 2 $,所以当 $ d= 55\sqrt 5 $ 时,$ \alpha - \beta $ 最大.故所求的 $ d $ 是 $ 55\sqrt 5 {\mathrm{m}} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2