如图,在四棱锥 $ P-ABCD $ 中,底面 $ ABCD $ 是矩形,$ PA\perp 平面ABCD $,$ AP=AB=2 $,$ BC= 2\sqrt 2 $,$ E $,$ F $ 分别是 $ AD $,$ PC $ 的中点.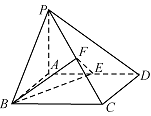

【难度】
【出处】
2010年高考陕西卷(理)
【标注】
-
证明:$ PC\perp 平面BEF $;标注答案解析解法一:如图,以 $ A $ 为坐标原点,$ AB $,$ AD $,$ AP $ 所在直线分别为 $ x $,$ y $,$ z $ 轴建立空间直角坐标系.
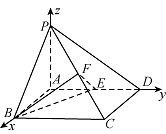 $\because$ $AP = AB = 2$,$BC = AD = 2\sqrt 2 $,四边形 $ ABCD $ 是矩形,
$\because$ $AP = AB = 2$,$BC = AD = 2\sqrt 2 $,四边形 $ ABCD $ 是矩形,
$\therefore$ $ A $,$ B $,$ C $,$ D $,$ P $ 的坐标为 $A\left(0,0,0\right),B\left(2,0,0\right),C\left(2,2\sqrt 2 ,0\right),D\left(0,2\sqrt 2 ,0\right),P\left(0,0,2\right)$,
又 $ E $,$ F $ 分别是 $ AD $,$ PC $ 的中点,$\therefore$ $E\left(0,\sqrt 2 ,0\right),F\left(1,\sqrt 2 ,1\right)$,
所以\[\overrightarrow {PC} = \left(2,2\sqrt 2 , - 2\right),\overrightarrow {BF} = \left( - 1,\sqrt 2 ,1\right),\overrightarrow {EF} = \left(1,0,1\right),\]所以\[\overrightarrow {PC}\cdot \overrightarrow {BF} = - 2 + 4 - 2 = 0,\overrightarrow {PC} \cdot\overrightarrow {EF} = 2 + 0 - 2 = 0,\]所以\[\overrightarrow {PC} \bot \overrightarrow {BF} ,\overrightarrow {PC} \bot \overrightarrow {EF} ,\]所以\[\overrightarrow {PC} \bot \overrightarrow {BF} ,\overrightarrow {PC} \bot \overrightarrow {EF} ,BF \cap EF = F,\]所以 $PC \perp平面 BEF$.
解法二:如图,连接 $ PE $,$ EC $,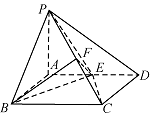 在 ${\rm{Rt}}\triangle PAE$ 和 ${\rm{Rt}}\triangle CDE$ 中,
在 ${\rm{Rt}}\triangle PAE$ 和 ${\rm{Rt}}\triangle CDE$ 中,
$ PA=AB=CD $,$ AE=DE $,
$\therefore$ $ PE=CE $,即 $\triangle PEC$ 是等腰三角形,
又 $ F $ 是 $ PC $ 的中点,$\therefore$ $ EF\perp PC $,
又 $BF = \sqrt {A{P^2} + A{B^2}} = 2\sqrt 2 = BC,F$ 是 $ PC $ 的中点,
$\therefore$ $BF \perp PC$,
又 $BF \cap EF = F$ $ \therefore $ $PC \perp 平面BEF$. -
求平面 $ BEF $ 与平面 $ BAP $ 夹角的大小.标注答案解析解法一:由(1)知平面 $ BEF $ 的法向量\[\overrightarrow {n_1} = \overrightarrow {PC} = \left(2,2\sqrt 2 , - 2\right),\]平面 $ BAP $ 的法向量\[\overrightarrow {n_2} = \overrightarrow {AD} = \left(0,2\sqrt 2 ,0\right),\]$\therefore$ $\overrightarrow {n_1}\cdot\overrightarrow {n_2} =8$,
设平面 $ BEF $ 与平面 $ BAP $ 的家教为 $ θ $,则\[\begin{split}\cos \theta &= \left|\cos \left(\overrightarrow {n_1},\overrightarrow {n_2}\right) \right| = \dfrac{{ \left|\overrightarrow {n_1}\cdot\overrightarrow {n_2} \right|}}{{ \left|\overrightarrow {n_1} \right| \left|\overrightarrow {n_2} \right|}} \\&= \dfrac{8}{{4 \times 2\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2},\end{split}\]$\therefore$ $\theta = {45^ \circ }$,$\therefore$ 平面 $ BEF $ 与平面 $ BAP $ 的夹角为 ${45^ \circ }$.
解法二:$\because$ $ PA\perp 平面 ABCD $,$\therefore$ $ PA\perp BC $,
又 $ ABCD $ 是矩形,$\therefore$ $ AB\perp BC $,
$\therefore$ $ BC\perp 平面BAP $,$ BC\perp PB $,又由(I)知 $ PC\perp 平面BEF $,
$\therefore$ 直线 $ PC $ 与 $ BC $ 的夹角即为平面 $ BEF $ 与平面 $ BAP $ 的夹角,
在 $\triangle PBC$ 中,$ PB=BC $,$\angle PBC = {90^ \circ }$,$\angle PCB = {45^ \circ }$,
所以平面 $ BEF $ 与平面 $ BAP $ 的夹角为 ${45^ \circ }$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2