某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 $\dfrac{{80{\mathrm{\pi }}}}{3}$ 立方米,且 $l \geqslant 2r$.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 $3$ 千元,半球形部分每平方米建造费用为 $c \left( {c > 3} \right)$ 千元.设该容器的建造费用为 $y$ 千元.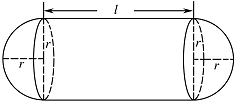

【难度】
【出处】
无
【标注】
-
写出 $y$ 关于 $r$ 的函数表达式,并求该函数的定义域;标注答案解析由题意可知\[{\mathrm{\pi }}{r^2}l + \dfrac{{4{\mathrm{\pi }}}}{3}{r^3} = \dfrac{{80}}{3}{\mathrm{\pi }}\left(l \geqslant 2r\right),\]即\[l = \dfrac{{80}}{{3{r^2}}} - \dfrac{4}{3}r \geqslant 2r,\]则\[0 < r \leqslant 2.\]容器的建造费用为\[\begin{split}y & = 2{\mathrm{\pi }}rl \times 3 + 4{\mathrm{\pi }}{r^2} \times c \\& = 6{\mathrm{\pi }}r\left( {\dfrac{{80}}{{3{r^2}}} - \dfrac{4}{3}r} \right) + 4{\mathrm{\pi }}{r^2}c,\end{split}\]即\[y = \dfrac{{160{\mathrm{\pi }}}}{r} - 8{\mathrm{\pi }}{r^2} + 4{\mathrm{\pi }}{r^2}c,\]定义域为\[\left\{ {r\left| {0 < r \leqslant 2} \right.} \right\}.\]
-
求该容器的建造费用最小时的 $r$.标注答案解析由(1)得\[\begin{split}y' & = - \dfrac{{160{\mathrm{\pi }}}}{{{r^2}}} - 16{\mathrm{\pi }}r + 8{\mathrm{\pi }}rc \\& = \dfrac{{8{\mathrm{\pi }}\left( {c - 2} \right)}}{{{r^2}}}\left( {{r^3} - \dfrac{{20}}{{c - 2}}} \right),0 < r \leqslant 2,\end{split}\]由于 $c > 3$,所以 $c - 2 > 0$,当\[{r^3} - \dfrac{{20}}{{c - 2}} = 0 , r = \sqrt[3]{{\dfrac{{20}}{{c - 2}}}}.\]令 $r = \sqrt[3]{{\dfrac{{20}}{{c - 2}}}} = m$,则 $m > 0$,所以\[y' = \dfrac{{8{\mathrm{\pi }}\left( {c - 2} \right)}}{{{r^2}}}\left( {r - m} \right)\left( {{r^2} + rm + {m^2}} \right).\]① 当 $0 < m < 2$ 即 $c > \dfrac{9}{2}$ 时,
当 $r = m$ 时,$y' = 0$;
当 $r \in \left( {0,m} \right)$ 时,$y' < 0$;
当 $r \in \left( {m,2} \right)$ 时,$y' > 0$;
所以 $r = m$ 是函数 $y$ 的极小值点,也是最小值点;
② 当 $m \geqslant 2$ 即 $3 < c \leqslant \dfrac{9}{2}$ 时,
当 $r \in \left( {0,2} \right)$ 时,$y' < 0$,函数单调递减,所以 $r = 2$ 是函数 $y$ 的最小值点.
综上所述,
当 $3 < c \leqslant \dfrac{9}{2}$ 时,建造费用最小时 $r = 2$;
当 $c > \dfrac{9}{2}$ 时,建造费用最小时 $r = \sqrt[3]{{\dfrac{{20}}{{c - 2}}}}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2