如图,$\triangle BCD$ 与 $\triangle MCD$ 都是边长为 $ 2 $ 的正三角形,平面 $MCD \perp 平面 BCD$,$AB \perp 平面 BCD$,$AB = 2\sqrt 3 $.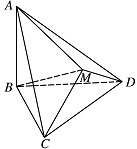

【难度】
【出处】
2010年高考江西卷(理)
【标注】
-
求点 $A$ 到平面 $MBC$ 的距离;标注答案解析解法一:如图,取 $ CD $ 中点 $ O $,连 $ OB $,$ OM $,
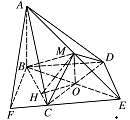 则 $ OB=OM=\sqrt3 $,$ OB\perp CD $,$ MO\perp CD $.
则 $ OB=OM=\sqrt3 $,$ OB\perp CD $,$ MO\perp CD $.
又平面 $ MCD\perp 平面 BCD$,则 $ MO\perp 平面 BCD $,
所以 $ MO\parallel AB $,$ MO\parallel 平面ABC $.
$ M $、$ O $ 到平面 $ ABC $ 的距离相等.
作 $ OH\perp BC $ 于 $ H $,连 $ MH $,则 $ MH\perp BC $.求得\[ \begin{split}OH&=OC\cdot \sin 60^\circ=\dfrac{\sqrt3}2 ,\\ MH&=\sqrt{\left(\sqrt3\right)+\left(\dfrac{\sqrt3}2\right)^2}=\dfrac{\sqrt{15}}2 .\end{split}\]设点 $ A$ 到平面 $ MBC$ 的距离为 $ d $,由 $V_{A-MBC}=V_{M-ABC} $,得\[\dfrac13\cdot S_{\triangle MBC}\cdot d=\dfrac13\cdot S_{\triangle ABC}\cdot OH ,\]即\[\dfrac13\times\dfrac12\times2\times\dfrac{\sqrt{15}}2d=\dfrac13\times\dfrac12\times2\times2\sqrt3\times\dfrac{\sqrt3}2, \]解得\[d=\dfrac{2\sqrt{15}}5 .\]解法二:取 $ CD $ 中点 $ O $,连 $ OB $,O $ M $,则 $ OB\perp CD $,$ OM\perp CD $.
又 $ 平面MCD\perp 平面BCD $,则 $ MO\perp 平面BCD$.
取 $ O $ 为原点,直线 $ OC $、$ BO $、$ OM $ 为 $ x $ 轴、$ y $ 轴、$ z $ 轴,建立空间直角坐标系如图.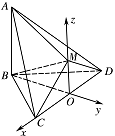 $ OB=OM=\sqrt3$,则各点坐标分别为 $ C(1,0,0) $,$ M(0,0,\sqrt3) $,$ B(0,-\sqrt3,0) $,$ A(0,-\sqrt3,2\sqrt3) $.
$ OB=OM=\sqrt3$,则各点坐标分别为 $ C(1,0,0) $,$ M(0,0,\sqrt3) $,$ B(0,-\sqrt3,0) $,$ A(0,-\sqrt3,2\sqrt3) $.
设 $\overrightarrow {{n_{}}} = \left(x,y,z\right)$ 是平面MBC的法向量,则 $\overrightarrow {BC} = \left(1,\sqrt 3 ,0\right)$,$\overrightarrow {BM} = \left(0,\sqrt 3 ,\sqrt 3 \right)$.
由 $\overrightarrow {{n_{}}} \bot \overrightarrow {BC} $ 得 $x + \sqrt 3 y = 0$;由 $\overrightarrow {{n_{}}} \bot \overrightarrow {BM} $ 得 $\sqrt 3 y + \sqrt 3 z = 0$.
取 $\overrightarrow {{n_{}}} = \left(\sqrt 3 , - 1,1\right)$,$\overrightarrow {BA} = \left(0,0,2\sqrt 3 \right)$,则\[d = \dfrac{{\left| {\overrightarrow {BA} \cdot \overrightarrow n } \right|}}{{\left| {\overrightarrow n } \right|}} = \dfrac{{2\sqrt 3 }}{{\sqrt 5 }} = \dfrac{{2\sqrt {15} }}{5}.\] -
求平面 $ACM$ 与平面 $BCD$ 所成二面角的正弦值.标注答案解析解法一:
延长 $ AM $、$ BO $ 相交于 $ E $,连 $ CE $、$ DE $,$ CE $ 是平面 $ACM $ 与平面 $ BCD$ 的交线.
由(1)知,$ O $ 是 $ BE $ 的中点,则 $ BCED $ 是菱形.
作 $ BF\perp EC $ 于 $ F $,连 $ AF $,则 $ AF\perp EC $,
$ \angle AFB $ 就是二面角 $ A-EC-B $ 的平面角,设为 $\theta $.
因为 $ \angle BCE=120^\circ $,所以 $ \angle BCF=60^\circ $.
所以 $BF = BC \cdot \sin {60^ \circ } = \sqrt 3 $,
所以 $\tan \theta = \dfrac{{AB}}{{BF}} = 2$,$\sin \theta = \dfrac{{2\sqrt 5 }}{5}$,
所以,所求二面角的正弦值是 $\dfrac{{2\sqrt 5 }}{5}$.
解法二:
$\overrightarrow {CM} = \left( - 1,0,\sqrt 3 \right)$,$\overrightarrow {CA} = \left( - 1, - \sqrt 3 ,2\sqrt 3 \right)$.
设平面 $ ACM $ 的法向量为 $\overrightarrow {{n_1}} = \left(x,y,z\right)$,由\[{\begin{cases}
\overrightarrow {{n_1}} \perp \overrightarrow {CM}, \\
\overrightarrow {{n_1}} \perp \overrightarrow {CA} ,\\
\end{cases}}\]得\[{\begin{cases}- x + \sqrt 3 z = 0 ,\\
- x - \sqrt 3 y + 2\sqrt 3 z = 0 ,\\
\end{cases}}\]解得 $x = \sqrt 3 z$,$y = z$,取 $\overrightarrow {{n_1}} = \left(\sqrt 3 ,1,1\right)$.
又平面 $ BCD $ 的法向量为 $\overrightarrow n = \left(0,0,1\right)$,则\[\cos \left \langle\overrightarrow {{n_1}} ,\overrightarrow n \right\rangle= \dfrac{{\overrightarrow {{n_1}} \cdot \overrightarrow n }}{{ \left| {\overrightarrow n_1 } \right| \cdot \left| {\overrightarrow n } \right|}} = \dfrac{1}{{\sqrt 5 }}.\]设所求二面角为 $\theta $,则\[\sin \theta = \sqrt {1 - {{\left(\dfrac{1}{{\sqrt 5 }}\right)}^2}} = \dfrac{{2\sqrt 5 }}{5}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2