如图,在长方体 $ ABCD-A_{1}B_{1}C_{1}D_{1} $ 中,$ E $,$ H $ 分别是棱 $ A_{1}B_{1} $,$ D_{1}C_{1} $ 上的点(点 $ E $ 与 $ B_{1} $ 不重合),且 $ EH\parallel A_{1} D_{1} $.过 $ EH $ 的平面与棱 $ BB_{1} $,$ CC_{1} $ 相交,交点分别为 $ F $,$ G $.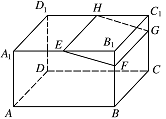

【难度】
【出处】
2010年高考福建卷(文)
【标注】
-
证明:$ AD\parallel 平面 EFGH $;标注答案解析在长方体 $ ABCD-A_{1}B_{1}C_{1}D_{1} $ 中,$ AD\parallel A_{1} D_{1 } $.
又 $\because$ $ EH\parallel A_{1} D_{1 } $,$\therefore$ $ AD\parallel EH $.
$\because$ $ AD \not\subset 平面 EFGH $,$ EH \subset 平面 EFGH $,
$\therefore$ $ AD\parallel 平面 EFGH $. -
设 $ AB=2AA_{1} =2 a $.在长方体 $ ABCD-A_{1}B_{1}C_{1}D_{1} $ 内随机选取一点.记该点取自几何体 $ A_{1}ABFE-D_{1}DCGH $ 内的概率为 $ p $,当点 $ E $,$ F $ 分别在棱 $ A_{1}B_{1} $,$B_1B$ 上运动且满足 $ EF=a $ 时,求 $ p $ 的最小值.标注答案解析设 $ BC=b $,则长方体 $ ABCD-A_{1}B_{1}C_{1}D_{1} $ 的体积\[V=AB\cdot AD\cdot AA_{1} =2a^2b,\]几何体 $ EB_{1}F-HC_{1}G $ 的体积\[V_{1} =\left(\dfrac 1 2 EB_{1 }\cdot B_{1}F\right)\cdot B_{1}C_{1} =\dfrac b 2 \cdot EB_{1} \cdot B_{1 }F.\]因为\[EB_{1}^2 + B_{1 }F^2=a^2,\]所以\[EB_{1}\cdot B_{1 }F\leqslant \dfrac {EB_{1}^2 + B_{1 }F^2_{ }} 2 = \dfrac {a^2} 2 ,\]当且仅当 $ EB_{1} =B_{1 }F=\dfrac {\sqrt 2} 2 a $ 时等号成立.从而\[V_{1} \leqslant \dfrac {a^2b} 4 .\]故\[p=1-\dfrac {V_1} V \geqslant 1 - \dfrac{{\dfrac{{{a^2}b}}{4}}}{{2{a^2}b}} = \dfrac{7}{8}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2