在如图所示的几何体中,四边形 $ABCD$ 是正方形,$MA \perp 平面 ABCD$,$PD\parallel MA$,$E$、$G$、$F$ 分别为 $MB$、$PB$、$PC$ 的中点,且 $AD =PD = 2MA$.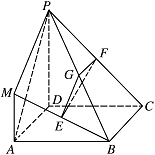

【难度】
【出处】
2010年高考山东卷(文)
【标注】
-
求证:$ 平面 EFG \perp 平面PDC$;标注答案解析由已知 $ MA \perp平面 ABCD $,$ PD \parallel MA $,
所以 $ PD\perp平面 ABCD $.
又 $ BC \subset 平面 ABCD $,所以 $ PD\perp BC $.
因为四边形 $ ABCD $ 为正方形,所以 $ BC\perp DC $.
又 $ PD\cap DC=D $,因此 $ BC\perp 平面 PDC $,
在 $ \triangle PBC $ 中,因为 $ G $,$F$ 分别为 $PB$,$ PC $ 的中点,
所以 $ GF\parallel BC $,因此 $ GF\perp 平面 PDC $.
又 $ GF \subset 平面 EFG $,所以 $ 平面 EFG\perp 平面 PDC $. -
求三棱锥 $P - MAB$ 与四棱锥 $P - ABCD$ 的体积之比.标注答案解析因为 $ PD\perp 平面 ABCD $,四边形 $ ABCD $ 为正方形,不妨设 $ MA=1 $,
则 $ PD=AD=2 $,所以\[ V_{P-ABCD}=\dfrac13S_{正方形 ABCD}\cdot PD=\dfrac 83. \]由于 $ DA\perp 面 MAB $,且 $ PD\parallel MA$,所以 $ DA $ 即为点 $ P $ 到平面 $ MAB $ 的距离,所以\[ V_{P-MAB}=\dfrac13\times \dfrac12\times 1\times 2\times 2=\dfrac23, \]故\[ V_{P-MAB}:V_{P-ABCD}= 1:4. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2