如图,已知椭圆 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1{ }\left(a > b > 0\right)$ 过点.$\left(1,\dfrac{\sqrt 2 }{2}\right)$,离心率为 $\dfrac{\sqrt 2 }{2}$,左、右焦点分别为 ${F_1}$、${F_2}$.点 $P$ 为直线 $l:x + y = 2$ 上且不在 $x$ 轴上的任意一点,直线 $P{F_1}$ 和 $P{F_2}$ 与椭圆的交点分别为 $A$,$B$ 和 $C$,$D$,$O$ 为坐标原点.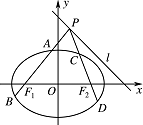

【难度】
【出处】
2010年高考山东卷(文)
【标注】
-
求椭圆的标准方程;标注答案解析因为椭圆过点 $\left(1,\dfrac{\sqrt 2 }{2} \right)$,$e=\dfrac{\sqrt 2 }{2}$,所以\[\dfrac{1}{a^2} + \dfrac{1}{{2{b^2}}} = 1,\dfrac{c}{a} = \dfrac{\sqrt 2 }{2}.\]又 ${a^2} = {b^2} + {c^2}$,所以\[a = \sqrt 2 ,b = 1,c = 1,\]故所求椭圆方程为\[\dfrac{x^2}{2} + y^2 = 1.\]
-
设直线 $P{F_1}$、$P{F_2}$ 的斜率分别为 ${k_1}$、${k_2}$.
(i)证明:$\dfrac{1}{k_1} - \dfrac{3}{k_2} = 2$;
(ii)问直线 $l$ 上是否存在点 $P$,使得直线 $OA$、$OB$、$OC$、$OD$ 的斜率 ${k_{OA}}$、${k_{OB}}$、${k_{OC}}$、${k_{OD}}$ 满足 ${k_{OA}} + {k_{OB}} + {k_{OC}} + {k_{OD}} = 0$?若存在,求出所有满足条件的点 $P$ 的坐标;若不存在,说明理由.标注答案解析(i)方法一:因为 $ F_1\left(-1,0\right)$,$F_2\left(1,0\right) $,$PF_1 $,$ PF_2$ 的斜率分别为 $ k_1$,$k_2 $,
且点 $ P$ 不在 $x $ 轴上,所以 $k_1\neq k_2 $,$ k_1\neq0$,$ k_2\neq0$.
又直线 $PF_1 $,$ PF_2$ 的方程分别为\[y=k_1\left(x+1\right) ,y=k_2\left(x-1\right) ,\]联立两方程解得\[\begin{cases}x=\dfrac{k_1+k_2}{k_2-k_1},\\y=\dfrac{2k_1k_2}{k_2-k_1}, \end{cases}\]所以 $ P\left(\dfrac{k_1+k_2}{k_2-k_1},\dfrac{2k_1k_2}{k_2-k_1}\right)$,由于点 $ P$ 在直线 $ x+y=2$ 上,所以\[\dfrac{k_1+k_2+2k_1k_2}{k_2-k_1}=2 ,\]因此\[ 2k_1k_2+3k_1-k_2=0,\]即\[\dfrac1k_1-\dfrac3k_2=2 ,\]结论成立.
方法二:设 $ P\left(x_0,y_0\right)$,则\[ k_1=\dfrac{y_0}{x_0+1},k_2=\dfrac{y_0}{x_0-1},\]因为点 $P $ 不在 $x $ 轴上,所以 $y_0\neq0 $.
又 $x_0+y_0=2 $,所以\[\begin{split}\dfrac1k_1-\dfrac3k_2&=\dfrac{x_0+1}{y_0}-\dfrac{3\left(x_0-1\right)}{y_0}\\&=\dfrac{4-2x_0}{y_0}=\dfrac{2y_0}{y_0}=2.\end{split} \]因此结论成立.
(ii)设 $A\left({x_A},{y_A}\right)$,$B\left({x_B},{y_B}\right)$,$C\left({x_C},{y_C}\right)$,$D\left({x_D},{y_D}\right)$.
联立直线 $ PF_1$ 与椭圆的方程得\[\begin{cases} y=k_1\left(x+1\right),\\ \dfrac{x^2}2+y^2=1,\end{cases}\]化简得\[ \left(2k_1^2+1\right)x^2+4k_1^2x+2k_1^2-2=0,\]因此\[ x_A+x_B=\dfrac{-4k_1^2}{2k_1^2+1},x_Ax_B=\dfrac{2k_1^2-2}{2k_1^2+1}.\]由于 $OA $,$OB $ 的斜率存在,所以 $x_A\neq0 $,$ x_B\neq0$,因此 $k_1^2\neq0 $ 且 $k_1^2\neq1 $.
因此\[ \begin{split}k_{OA}+k_{OB}&=\dfrac{y_A}{x_A}+\dfrac{y_B}{x_B}=\dfrac{k_1\left(x_A+1\right)}{x_A}+\dfrac{k_1\left(x_B+1\right)}{x_B}\\&=2k_1+k_1\cdot\dfrac{x_A+x_B}{x_Ax_B}=k_1\left(2-\dfrac{4k_1^2}{2k_1^2-2}\right)\\&=-\dfrac{4k_1}{2k_1^2-2}=-\dfrac{2k_1}{k_1^2-1}.\end{split}\]类似地可以得到 $ x_C\neq0$,$x_D\neq0 $,$ k_2^2\neq0$ 且 $k_2^2\neq1 $.所以\[k_{OC}+k_{OD}=-\dfrac{2k_2}{k_2^2-1} ,\]故\[\begin{split}{k_{OA}} + {k_{OB}} + {k_{OC}} + {k_{OD}} &= \left(\dfrac{k_1}{k_1^2 - 1} + \dfrac{k_2}{k_2^2 - 1}\right)\\&= - 2\dfrac{{{k_1}k_2^2 - {k_1} + k_1^2{k_2} - {k_2}}}{\left(k_1^2 - 1\right)\left(k_2^2 - 1\right)}\\& = - \dfrac{{2\left({k_1}{k_2} - 1\right)\left({k_1} + {k_2}\right)}}{\left(k_1^2 - 1\right)\left(k_2^2 - 1\right)}.\end{split}\]若 ${k_{OA}} + {k_{OB}} + {k_{OC}} + {k_{OD}} = 0$,须有\[{k_1} + {k_2}=0 或 {k_1}{k_2}=1.\]① 当 ${k_1} + {k_2}=0$ 时,结合(ⅰ)的结论,可得 ${k_2}=-2$,所以解得点 $ P $ 的坐标为 $ \left(0,2\right) $;
② 当 ${k_1}{k_2} =1$ 时,结合(ⅰ)的结论,可得 ${k_2} =3 或 {k_2}=-1$(此时 ${k_1} =-1$,不满足 ${k_1}\neq {k_2}$,舍去),
此时直线 $ CD $ 的方程为 $y = 3\left(x - 1\right)$,联立方程 $x + y = 2$ 得 $x = \dfrac{5}{4}$,$y = \dfrac{3}{4}$,因此 $P\left(\dfrac{5}{4},\dfrac{3}{4}\right)$.
综上所述,满足条件的点 $ P $ 的坐标分别为 $\left(0,2\right)$,$\left(\dfrac{5}{4},\dfrac{3}{4}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2