设函数 $f\left(x\right) = \left| {2x - \left. 4 \right|} \right. + 1$.

【难度】
【出处】
2010年高考新课标全国卷(文)
【标注】
-
画出函数 $y= f\left(x\right)$ 的图像;标注答案解析由于\[f\left(x\right) = \begin{cases}
{ - 2x + 5,x < 2} ,\\
{2x - 3,x \geqslant 2},
\end{cases} \]则函数 $y = f\left(x\right)$ 的图像如图所示.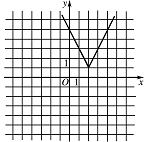
-
若不等式 $f\left(x\right) \leqslant ax$ 的解集非空,求 $ a $ 的取值范围.标注答案解析由函数 $y = f\left(x\right)$ 与函数 $y = ax$ 的图像可知,当且仅当 $a < - 2 或 a \geqslant \dfrac 1 2 $ 时,
函数 $y = f\left(x\right)$ 与函数 $y = ax$ 的图像有交点.
故不等式 $f\left(x\right) \leqslant ax$ 的解集非空时,$ a $ 的取值范围为 $\left( { - \infty , - 2} \right) \cup \left[\dfrac{1}{2}, + \infty \right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2