如图,椭圆 $C:\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ 的顶点为 ${A_1},{A_2},{B_1},{B_2}$,焦点为 ${F_1},{F_2}$,$|{A_1}{B_1}| = \sqrt 7 $,${S_{平行四边形{A_1}{B_1}{A_2}{B_2}}} = 2{S_{平行四边形{B_1}{F_1}{B_2}{F_2}}}$.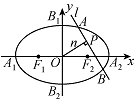

【难度】
【出处】
2010年高考陕西卷(文)
【标注】
-
求椭圆 $ C $ 的方程;标注答案解析由 $|{A_1}{B_1}| = \sqrt 7 $,知\[{a^2} + {b^2} = 7, \quad \cdots \cdots ① \]由 ${S_{平行四边形{A_1}{B_1}{A_2}{B_2}}} = 2{S_{平行四边形{B_1}{F_1}{B_2}{F_2}}}$,知\[ a=2c, \quad \cdots \cdots ② \]又\[{b^2} = {a^2} - {c^2}, \quad \cdots \cdots ③ \]由 $ ①②③ $ 解得 ${a^2} = 4,{b^2} = 3$,故椭圆 $ C $ 的方程为\[\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1.\]
-
设 $ n $ 为过原点的直线,$l$ 是与 $ n $ 垂直相交于 $ P $ 点,与椭圆相交于 $ A $,$ B $ 两点的直线,$\left| {\overrightarrow {OP} } \right| = 1$.是否存在上述直线 $l$ 使 $\overrightarrow {OA} \cdot \overrightarrow {OB} = 0$ 成立?若存在,求出直线 $l$ 的方程;若不存在,请说明理由.标注答案解析设 $ A $,$ B $ 两点的坐标分别为 $\left({x_1},{y_1}\right),\left({x_2},{y_2}\right)$,假设使 $\overrightarrow {OA} \cdot\overrightarrow {OB} = 0$ 成立的直线 $l$ 存在,
(ⅰ)当 $l$ 不垂直于 $ x $ 轴时,设 $l$ 的方程为 $y = kx + m$,
由 $l$ 与 $n$ 垂直相交于 $ P $ 点且 $ \left|\overrightarrow {OP} \right|=1$,得\[\dfrac{|m|}{{\sqrt {1 + {k^2}} }} = 1,\]即\[{m^2} = {k^2} + 1.\]因为\[\overrightarrow{OA}\cdot\overrightarrow{OB}={x_1}{x_2} + {y_1}{y_2} = 0,\]将 $y = kx + m$ 代入椭圆方程,得\[\left(3 + 4{k^2}\right){x^2} + 8kmx + \left(4{m^2} - 12\right) = 0,\]由求根公式可得\[{x_1} + {x_2} = \dfrac{ - 8km}{{3 + 4{k^2}}}, \quad \cdots \cdots ④ \\ {x_1}{x_2} = \dfrac{{4{m^2} - 12}}{{3 + 4{k^2}}}, \quad \cdots \cdots ⑤ \]且\[\begin{split}0 &= {x_1}{x_2} + {y_1}{y_2}\\& = {x_1}{x_2} + \left(k{x_1} + m\right)\left(k{x_2} + m\right)\\&={x_1}{x_2} + {k^2}{x_1}{x_2} + km\left({x_1} + {x_2}\right) + {m^2}\\&=\left(1 + {k^2}\right){x_1}{x_2} + km\left({x_1} + {x_2}\right) + {m^2},\end{split}\]将 $ ④⑤ $ 代入上式并化简得\[\left(1 + {k^2}\right)\left(4{m^2} - 12\right) - 8{k^2}{m^2} + {m^2}\left(3 + 4{k^2}\right) = 0, \quad \cdots \cdots ⑥ \]将 ${m^2} = 1 + {k^2}$ 代入 $ ⑥ $ 并化简得 $ - 5\left({k^2} + 1\right) = 0$,矛盾.即此时直线 $l$ 不存在.
(ii)当 $l$ 垂直于 $x$ 轴时,满足 $\left| \overrightarrow {OP} \right|= 1 $ 的直线 $l$ 的方程为 $x = 1 或 x = - 1$,
则 $ A $,$ B $ 两点的坐标为 $\left(1,\dfrac{3}{2}\right),\left(1, - \dfrac{3}{2}\right),$ 或 $\left( - 1,\dfrac{3}{2}\right),\left( - 1, - \dfrac{3}{2}\right),$
当 $x = 1$ 时,$\overrightarrow {OA} \cdot\overrightarrow {OB} = \left(1,\dfrac{3}{2}\right)\cdot\left(1, - \dfrac{3}{2}\right) = - \dfrac{5}{4} \ne 0;$
当 $x = - 1$ 时,$\overrightarrow {OA} \cdot\overrightarrow {OB} = \left( - 1,\dfrac{3}{2}\right)\cdot\left( - 1, - \dfrac{3}{2}\right) = - \dfrac{5}{4} \ne 0;$
所以此时直线 $l$ 也不存在.
综上可知,使 $\overrightarrow {OA} \cdot\overrightarrow {OB} = 0$ 成立的直线 $l$ 不存在.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2