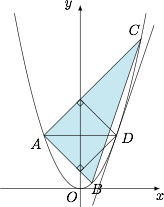
题目 设 $A,B,C,D$ 为抛物线 ${x^2} = 4y$ 上不同的四点，$A,D$ 关于该抛物线的对称轴对称，$BC$ 平行于该抛物线在点 $D$ 处的切线 $l$．设 $D$ 到直线 $AB$，直线 $AC$ 的距离分别为 ${d_1},{d_2}$，已知 ${d_1} + {d_2} = \sqrt 2 \left| {AD} \right|$． 问题1 判断 $\triangle ABC$ 是锐角三角形、直角三角形、钝角三角形中的哪一种三角形，并说明理由； 答案1 直角三角形 解析1 由题意，设$$A\left( { - {x_0}, {y_0}} \right),D\left( {{x_0}, {y_0}} \right),B\left( {{x_1}, {y_1}} \right),C\left( {{x_2}, {y_2}} \right),$$则切线方程为$${x_0}x = 2\left( {y + {y_0}} \right),$$所以切线斜率为 $\dfrac{{{x_0}}}{2}$，于是$${k_{BC}} = \dfrac{{{x_0}}}{2} , {k_{AC}} = \dfrac{{{y_2} - {y_0}}}{{{x_2} + {x_0}}} = \dfrac{{{x_2} - {x_0}}}{4},$$所以$${k_{AB}} = \dfrac{{{x_1} - {x_0}}}{4} , {k_{BC}} = \dfrac{{{x_1} + {x_2}}}{4}=\dfrac {x_0}2,$$因此$${k_{AC}} + {k_{AB}} = \dfrac{{{x_2} + {x_1} - 2{x_0}}}{4} = 0 , {k_{AC}} = - {k_{AB}}.$$<img src="/static/images/c7a294a3b75d733ac4c79c56e4d1b4ed.png" class="img-responsive" />从而$${d_1} = {d_2},$$又$${d_1} + {d_2} = \sqrt 2 AD,$$所以$$\angle BAD = \angle CAD = 45^\circ ,$$所以 $\triangle ABC$ 为直角三角形． 备注1 问题2 若 $\triangle ABC$ 的面积为 $240$，求点 $A$ 的坐标及直线 $BC$ 的方程． 答案2 $A\left( { \pm 8, 16} \right)$；$BC$ 方程为 $y = \pm 4x - 12$ 解析2 由 $(1)$ 知，$${k_{AC}} = 1,{k_{AB}} = - 1,$$所以$${x_2} - {x_0} = 4,{x_1} - {x_0} = - 4,$$因此$$\begin{split}{S_{\triangle ABC}} &= \dfrac{1}{2}\left| {AC} \right| \cdot \left| {AB} \right|\\ &= \dfrac{1}{2}\sqrt 2 \left( {{x_2} + {x_0}} \right) \cdot \sqrt 2 \left( {{x_1} + {x_0}} \right)\\ &= \left( {4 + 2{x_0}} \right)\left( { - 4 + 2{x_0}} \right)\\ &= 240,\end{split}$$解得 ${x_0} = \pm 8$，于是 $A$ 点的坐标为 $\left( { \pm 8, 16} \right)$．<br/>所以对应的 $BC$ 方程为 $y = \pm 4x - 12$． 备注2